Adjoint Green’s Function for a Cylindrical Surface

Eq. (14.55) may be regarded as a particular solution of Eq. (14.53). There is also a homogeneous solution. When combining the particular and the homogeneous solution, the full solution satisfies boundary condition (14.51) on the cylindrical surface at r = D/2. In cylindrical coordinates, the appropriate homogeneous solution (denoted by a subscript “h”) is

(14.56)

where Cm is a set of unknown constants. H,(1) () is the mth order Hankel function of the first kind. By adding Eqs. (14.55) and (14.56), the adjoint Green’s function is

. i — (R —x cos 0 )+ШТ

= —Ше a° і 1 8n 2a0>R1

Upon imposing boundary condition (14.51), it is found that

Jm (a;sin 01 z)

»*{ a; si" 01D)

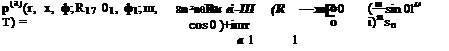Thus, the adjoint Green’s function p(a) and the radial velocity v(a) are

j~(t0 sin 0‘r) sin 01D)—sin D)sin 0-r

x cos[m^ — ф1)].

On the cylindrical surface, the terms inside the square bracket of Eq. (14.58) may be simplified by using the Wronskian relationship of Bessel functions. This gives

v(я) (D, x, ф; R1? 0Ь ф1; o, т)

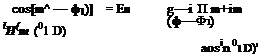By means of the reciprocity relation (14.52), the Fourier transform of the pres­sure of the surface Green’s function is given by the right-hand side of this equation. This expression may be further simplified by noting that

Therefore, by inverting the Fourier transform, the surface Green’s function becomes

p{g) ^,в, ф, t; D, Хо, Фо, т)

Eq. (14.59) is the same as the direct Green’s function of Eq. (14.18).