Phase delay

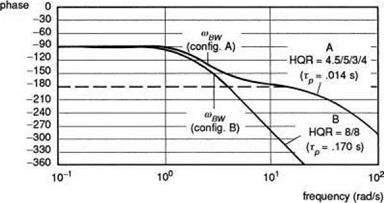
The quality of flying in the small amplitude-high frequency range of our framework diagram was initially encapsulated in a single-parameter bandwidth. Unfortunately, the situation turned out more complicated and it was not long before cases of equi- bandwidth configurations with widely varying handling qualities were found. Again, Hoh sheds light on this in Refs 6.23 and 6.24. For a wide variety of systems there is a unique relationship between the bandwidth frequency and the shape of the phase curve in the frequency domain beyond the bandwidth frequency. The steeper the phase ‘roll-off’, then the lower the bandwidth and, with relatively simple high-order effects like transport delays and actuator lags, the increasing phase slope correlates directly with bandwidth. However, for more general high-order dynamics, the phase delay has to be computed as an independent measure of handling, since configurations with markedly different phase slope can have the same bandwidth. A case is cited in Ref. 6.24 where two configurations with the same bandwidth were rated as Level 2 and 3, simply because the phase slopes were very different (Fig. 6.29). Pilots are particularly sensitive to the slope of the phase at high frequency, well beyond the bandwidth frequency but still within the range of piloting, e. g., > 10 rad/s. In a closed-loop tracking task, when high precision is required, pilots will find that high values of phase slope make it very difficult for them to adapt their control strategy to even small changes in frequency,

hence task disturbance. This and related effects reinforce the point that for tracking tasks the pilot is very sensitive to effects easily described in the frequency domain but hardly noticeable as delays following step inputs. The actual parameter selected to represent the shape of the phase is the phase delay, тp, defined as

where A®2®180 is the phase change between «180 and 2«180. The phase delay is therefore related to the slope of the phase between the crossover frequency and 2«180. Reference 6.5 notes that if the phase is nonlinear in this region, then the phase delay can be determined from a linear least-squares curve fit, in a similar way to the computation of equivalent time delay in LOES analysis.