Generation of a Random Broadband Acoustic Field

Many aeroacoustics problems involve noise generated by turbulence. For this class of problems, both the source and the sound field are random and consist of a broad spectrum of frequencies. This is the case of high-speed jet noise. At a high Reynolds number, the jet flow is turbulent with a wide range of length scales. The noise emitted is broadband typically spread over three decades of frequencies. At the present time, there are not enough computational resources to perform direct numerical simulations of the jet flow. Many investigators choose to use large eddy simulation (LES) as an alternative, but the computational domain is finite and often is minimized to reduce computational cost. For this reason, without exception, only the acoustic near field is computed. However, for community noise purposes, interest is in the far field. Therefore, a method capable of continuing broadband near acoustic field to the far field is very much needed.

In Appendix F, a method to produce real-time pressure waves from a random broadband noise source is described. For a broadband monopole source, the acoustic field generated is spherically symmetric. Consider such a localized source as shown in Figure 14.12. Suppose the noise spectrum S(s-D) is given where D is the length scale and a0 is the speed of sound. The sound field emitted by the monopole source following Appendix F is as follows:

(Ю

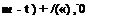
p(Y, t) = — A(m) cos

Figure 14.16. The similarity spectrum of the noise of large turbulence structures of high-speed jets. This spectrum is used as the noise spectrum of a broadband monopole source measured at Y/D = 1.0.
On following the energy-conserving discretization procedure, the discretized form of this equation is (see Eq. (F9)) as follows:
rnD a0
2S	(14.90)
p(Y, t)
j
j
a0
As a numerical example, suppose the noise spectrum S(sD) has the same shape as the similarity spectrum of the noise from the large turbulence structures of high­speed jets (see Tam, Golebiowski, and Seiner (1996); Tam, Viswanathan, Ahuja, and Panda (2008)). The similarity spectrum is shown in Figure 14.16. Note: the spectrum is assumed to be symmetric, i. e., S(-^) = S(^D). Upon dividing the spectrum into 250 bands, the spatial distribution of pressure in the wave field at a selected instant of time, according to Eq. (14.90), is shown in Figure 14.17. Figure 14.18 shows the time history of pressure fluctuations measured at a distance of Y = 5D from the monopole source. The random fluctuations are time stationary, that is, the stochastic properties of the broadband sound field is independent of time. An arbitrary starting time is used for the display in Figure 14.18.
Y/D
Figure 14.17. Spatial distribution of the pressure field of a broadband monopole source with a spectrum given by the sim­ilarity spectrum of Figure 14.16.

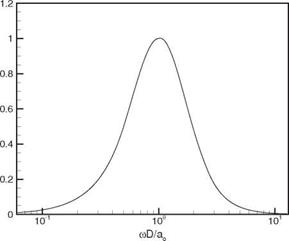
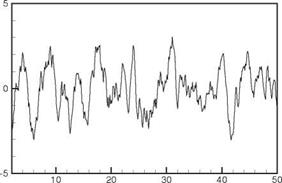
Figure 14.18. Time history of pressure fluctuations at Y = 5D from the broad­band monopole noise source of Figure 14.17.

The two-point space-time correlation function of the broadband sound field of a monopole source, following Eq. (F5), is given by

where the overbar means the time average. The function F(Y2 YD a°) can also be computed directly from the acoustic field of the monopole source, that is,

Y — Y —a t

Figure 14.19 shows the two-point space-time correlation function F ( 2 d 0 ) as computed directly according to Eq. (14.92). As a check on the accuracy of the energy – conserving discretization method and this formulation, the noise spectrum S(^D) is calculated by taking the Fourier transform of F(D), obtained by setting Y1 = Y2. This should yield the original prescribed similarity spectrum. A comparison of the two spectra is given in Figure 14.20. This figure indicates that there is good agreement between the two spectra. This confirms that the energy-conserving discretization method can, indeed, generate a broadband sound field with a given spectrum.