A Slightly Curved Foil in a Two-Dimensional Ground Effect

For the two-dimensional steady motion of a slightly curved foil near a flat ground plane, the corresponding singular integral equation has the form

й”рі 7«№-С, лЖ = -|г. (10.1)

where y(x) is the strength of vorticity that replaces the foil in the mathe­matical model, and dys/dx is a function that represents the slope of the foil camber line with respect to the horizontal axis;

IC(x-Z, h) = – (a. _ ^2 + 4/l2 = ^ _£)[(* _ £)2 + 4Л.2j (10-[59])

is the kernel of the integral equation. The first (singular) term of the kernel represents the contribution to the downwash from the foil-bound vorticity, whereas the second (regular) term accounts for the contribution of the down- wash from the vorticity of the foil mirror image. Abbreviation “v. p.” implies that the integral is understood in the sense of the Cauchy principal value.

We set the ground clearance h to zero and expand the kernel of the equa­tion in h. It can be seen that in the course of a straightforward expansion, the kernel would vanish to the lowest order. The second – and higher-order terms would contain divergent integrals. The principal difficulty in constructing this expansion is that parameter h is not always small compared to (x – £). To single out the subdomain x -£ = 0(h), we split the integral on the left-hand side of equation (10.1) into three integrals:

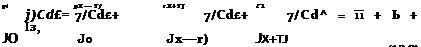1 =

where a small parameter r? is chosen so that h – C >) -C 1- It can be shown that contributions Ii and I3 are of the order О(h2), whereas the integral I2 = 0(h). In what follows, only the middle integral I2 will be retained, and Ii and I3 will be neglected.

For I2, the variable of integration varies in the range of x – r? <£< x + rj. We introduce a new stretched variable £ = (£ — x)/h, which has the order of 0(1). Then, _ _

(10.4)

Outside of the small vicinities of the edges (x = 0 and x — 1), the vortex density 7 can be expanded into a Taylor series

7(x + h£) = 7(x) + h£-y'(x) + – h2|27,,(x) + 0(/i3). (10.5)

Substituting this expansion in (10.5) gives

I2 = —4 h 7 ‘(x) arctan – j – + 0(h2).

Recalling that both h and T] should be small quantities with h = 0(1]), we can derive the following lowest order representation of the integral equation (10.1) for /1 —> 0:

*v<.>M

Thus, it has been shown that for very small relative ground clearances the integral equation for a foil-in-ground effect degenerates into a simple ordinary differential equation of the first order (10.7).

Recalling the relationship between the vortex density and the perturba­tion velocity potential tp,

d(p_ d(f+

^ dx dx ’

and assuming domination of the channel flow velocity potential, i. e., —

0(h(p~), it is easy to identify equation (10.7) with the equation (3.32), ob­tained by the matched asymptotics technique within the boundary problem formulation. The equivalence (to the lowest order) of boundary conditions for the aforementioned equations (10.7) and (3.33-3.34) follows from simple physical reasoning, namely,

• the circulation of the velocity Г(х) = f* 7(£)d£ should be zero at the leading edge, i. e., the potential at the leading edge should be continuous:

Г(1) = М1)-^+(1)*М1) = 0;