The General Potential Equation for Three-Dimensional Flow

For a steady, inviscid, three-dimensional flow, by continuity equation:

v • (pV) = 0,

that is:

d(pVx) д(рУу) д(руг)

dx ду dz

Euler’s equations of motion (neglecting body forces) are:

P

P

P

For incompressible flows, the density p is a constant. Therefore, the above four equations are sufficient for solving the four unknowns Vx, Vy, Vz and p. But for compressible flows, p is also an unknown. Therefore, the unknowns are p, Vx, Vy, Vz and p. Hence, the additional equation, namely, the isentropic process equation, is used. That is, pjpY = constant is the additional equation used along with continuity and momentum equations.

Introducing the potential function ф, we have the velocity components as:

дф дф дф

Vx = І = фХ, Vy = дф = фУ, Vz = І = фz.

Equation (9.37) may also be written as:

From isentropic process relation, p = p(p). Hence:

because from Equation (9.38a):

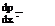( dVx dVx dVx ) dp

Vx —- + Vy —- + Vz—, —

^ dx y dy dz ) dp

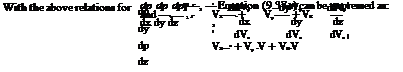Similarly:

dx ^	Vx2 1 – – Г a2	+1	Vy2 1 – -2 a2	) + Ї 0	V2 ) l – – j – a2 )	(V a2 ^ dy	d-y + ~-x
		–	-y-z ( a2 1	3Vy — ) dz dy )	Vz-x Г a2	—) , dx dz )	= 0.

Vx = — = фх, Vy = — = фу, Vz = — = фz дУ

But the velocity components and their derivatives in terms of potential function can be expressed as:

dVx dVy z

-x = фхх, – у = фуу, it = ф»

dVx – Vy – Vz

—- = фиУ, —– У = ф-к, —– = фzx-

ду xy dz yz dx zx

Therefore, in terms of potential function ф, the above equation can be expressed as:

t1 – a) ф“ + I1 – ал фуу + f1 – %)

This is the basic potential equation for compressible flow and it is nonlinear.

The difficulties associated with compressible flow stem from the fact that the basic equation is nonlinear. Hence the superposition of solutions is not valid. Further, in Equation (9.40) the local speed of sound ‘а is also a variable. By Equation (2.9e) of Reference 1, we have:

To solve a compressible flow problem, we have to solve Equation (9.40) using Equation (9.41), but this is not possible analytically. However, numerical solution is possible for given boundary conditions.