Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
CONSTANT PITCH
The idea of constant pitch has already been implied in the foregoing. For minimal profile drag, each small segment of a propeller blade should be set at the aerodynamic angle of attack which gives the best lift-drag ratio. What this angle is may be found from wind tunnel tests for the aerofoil section concerned. Since the profile changes from root to tip, ideally there should be a range of tunnel test results for a number of different points on the blade, and the eventual propeller layout should take account of these. On model propellers such precision is rarely found.
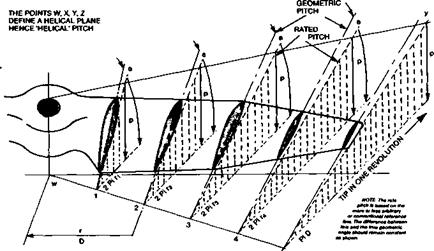
Whether or not the precise best angle for each aerofoil is known, the layout of a constant pitch propeller may be done by means of a diagram like that of Figure 14.6. Here, the desired pitch is represented on the vertical scale and expressed as a length (usually inches in English-speaking countries but centimetres or millimetres if SI units are used.) The basis of this figure is the notional distance the propeller would advance in one revolution if it were literally screwing itself through a solid medium like a screw or bolt This is, indeed, the origin of the words ‘airscrew’ and ‘pitch’ in this connection, by analogy with the pitch of the thread on a bolt. (The idea of ‘slip’ of a propeller as indicated in Figure 14.4, also originates here. Slip of a propeller blade is the angle of attack of the blade to the relative airflow and has no other meaning.) The distance that each segment of blade travels as the propeller rotates is represented by the horizontal scale. The extreme tip follows the circumference of a circle whose length is found from the standard circle formula:
C = 3.142 x D
On such a diagram the same scale proportion must be used for both horizontal and vertical scales. By ruling a number of straight lines radiating from the lower comer of diagram, the actual pitch angles required at each point are found and may be transferred directly from the drawing to the propeller block or master blade for production. If correctly done, this produces a propeller which will have, at one airspeed and one rate of rotation, every part of the blade at the most efficient angle of attack. This is why such a propeller is termed ‘constant pitch’. At typical result is shown in Figure 14.7.
|
Fig. 14.7 Layout of a constant pitch propeller blade. The pitch, as a length, is represented by the vertical arrows. The distance round the hub travelled in one revolution is Pi x D at the tip and 2 Pi r at each radial Station. Drawing courtesy J. Lnenicka. |
It is clear from the above that at other airspeeds than the one for which the propeller is designed, even if the the rate of rotation is the same, the angle of attack will nowhere be at its best. This emphasises again that the propeller should be matched to the engine. It may be that a particular engine can turn a propeller of a certain diameter and pitch, at a certain rate. A model may be designed to fly at a speed which corresponds to this pitch. If, however, the model has more drag than anticipated it will not achieve the designed speed and the propeller will not be at its most efficient either. There is a double penalty. On the other hand, if the model drag is less than expected although a faster flight will result, the propeller will again not be at its best efficiency. A better result would be attained with a greater (coarser) pitch.
The constant pitch propeller just described is evidently ‘peaky’, in that it is designed foi best results at one speed and r. p.m. It is also efficient if the r. p.m. and flight speed vary ‘in step’ with one another, in a way that maintains the best angle of attack everywhere along the blade. This is indicated in Figure 14.8. There is at least a rough correspondence in reality since reduced engine power (low r. p.m.) results in lower flight speed. However, such a fortunate harmony is not likely to prevail at critical times. During take off, for instance, forward velocity is low and revolutions high. The coarse-pitch propeller blade is then at a higher angle of attack than optimum and may even stall (Fig. 14.9a). Racing aeroplanes have sometimes been incapable of taking off for this reason; the Schneider Trophy seaplane racers sometimes exemplifying this. Similarly, if, on a slow landing approach it becomes necessary to open the throttle to ‘go round again’ a stalled propeller could be disastrous. At the other end of the scale, a propeller designed for greatest efficiency in the take off mode, or climbing, will be working at lower angles of attack than optimum at high speed. Such a ‘fine pitch’ propeller will accelerate a model quickly from standstill but will lose efficiency rapidly as the airspeed increases (Fig. 14.9b).
