Pitch-to-roll and roll-to-pitch couplings

Pitch-roll and roll-pitch cross-couplings can be powerful and insidious. The natural sources of both are the gyroscopic and aerodynamic moments developed by the main rotor and, in dynamic manoeuvres with large attitude excursions, the uncommanded and sometimes unpredictable off-axis motion can require continuous attention by the pilot. Generally, the magnitude of the pitch-to-roll couplings are more severe than roll to pitch, due to the large ratio of pitch to roll moment of inertia, but are, arguably, more easily contained by the pilot, at least at low to moderate frequencies. Roll-to-pitch coupling effects can have a much stronger impact on flight path and speed control and hence handling qualities in moderate to large manoeuvres. From the results of a piloted simulation study on the NASA Flight Simulator for Advanced Aircraft (FSAA), Chen and Talbot (Ref. 6.80) hypothesized that the critical cross-coupling handling qualities parameters were the ratios of short-term steady-state roll (pitch) to pitch (roll) angular rates, approximated by the ratios of aerodynamic derivatives

Pilot HQRs were consistently awarded in the Level 2 area for values of the ratios greater than about 0.35. When the revision to MIL-H-8501 was initiated in the early 1980s, the

NASA results were initially used as the basis of new pitch-roll criteria. The derivative ratios clearly took no account of the control couplings, however, and were also difficult to measure with accuracy. After some refinement, the criteria adopted in ADS-33 were based on a time domain formulation, in terms of the ratio of the peak off-axis response to the desired on-axis response after 4 s following an abrupt step input, in the form

roll step^, pitch step^<±0.25 (Level 1), ±0.6 (Level 2) (6.35)

A series of additional piloted simulation and flight trials, conducted in the late 1980s at the Ames Research Center (Refs 6.81,6.82), confirmed the importance of the derivative ratios, but argued that the new ADS-33 criteria did not cater for the higher frequency control coupling effects, or the interaction with on-axis characteristics. With regard to control coupling, the data in Refs 6.81 and 6.82 suggested that equivalent rotor control phase angles of about 30° would lead to Level 3 handling, confirming the RAE results reported earlier in Ref. 6.17. The relationship between the ADS-33 criteria and the equivalent linear system parameters can be illustrated using the simple first-order rate response formulation (Ref. 6.83), given by the equations

The relationship between the ADS-33 criteria and the parameters in eqns 6.36 and 6.37 can be reduced to the form

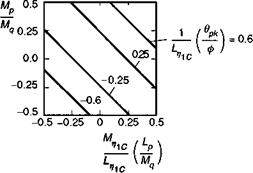
indicating that the pitch attitude coupling in a roll manoeuvre is dependent on both the cross-damping ratio of Ref. 6.80 (Mp/Mq) and the control sensitivity ratio scaled by the ratio of roll to pitch damping. Even with a zero value for the rate coupling Mp, control couplings can give rise to similar levels of pitch attitude excursion. The ADS time domain parameter in this simple model is therefore linearly related to the derivative ratios Mp/Mq and Mmc/Lmc. Given the roll axis control sensitivity and bandwidth, the importance of the control coupling is therefore inversely proportional to the pitch attitude bandwidth, Mq, hence emphasizing the importance of pitch axis effectiveness in cancelling coupling effects. Contours of equal ADS response are therefore given as shown in Fig. 6.67.

Our understanding of the handling qualities effects of roll-pitch coupling has been significantly extended by the series of flight/simulation experiments conducted by the US Army/DLR in the early 1990s, with support from DRA. The work to date is reported in Refs 6.84 and 6.85 and has focused on evaluating handling qualities in forward flight MTEs typified by the lateral slalom. In Ref. 6.84, couplings are classified into three types – those due to rate and control effects and the so-called washed-out coupling effects, more typical of augmented rotorcraft. Reference 6.85 concludes that the current ADS format is adequate for discriminating against unacceptable characteristics in the

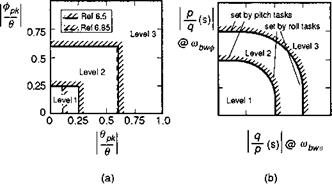
first two categories, but not the washed-out effects, which appear to be frequency dependent. However, data are presented in Ref. 6.85 which suggest a modification to the ADS Level 1/2 boundary as shown in Fig. 6.68(a), where the acceptable level of coupling has been reduced to 0.1. A new frequency domain criterion is proposed in Ref. 6.85 which appears to give a more consistent picture for all three types of coupling. The general form of the criterion is presented in Fig. 6.68(b), where the key parameters are the magnitudes of the frequency response functions between pitch (roll) and roll (pitch) rates, evaluated at the bandwidth of the off-axis attitude response. This format, therefore, again reflects the importance of the response characteristics in the coupled axis. Strictly, the data from Ref. 6.85 will define only the vertical portions of the boundaries in Fig. 6.68(b): the author has hypothesized the upper, horizontal boundaries, which would be defined for pitch axis tasks, and the curved boundary between, reflecting the additional degradation in multi-axis tasks, when couplings in both axes are present.

6.7.1 Collective to pitch coupling

At high speed, the application of main rotor collective pitch can generate powerful pitch and roll moments on the fuselage. Experiments to quantify the effects of collective to pitch coupling on handling qualities were reported in Ref. 6.86. The results were not conclusive but did indicate the powerful degrading effect, sending HQRs across the full span of the Level 2 range as the coupling parameter increased. ADS-33 reflects the limited dataset for collective to attitude couplings and sets limits on the pitch attitude change occurring within 3 s of an abrupt collective input. The limits are set as the ratio of pitch attitude change to the corresponding change in normal acceleration and take the form

where the negative value in eqn 6.40 corresponds to down collective inputs. The above criteria apply to forward flight. In low-speed flight the emphasis is more on the collective to yaw couplings.