Use of Karman Rule

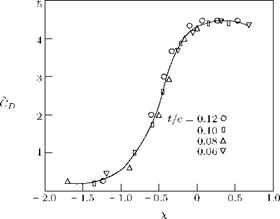
If we know the solution for one profile, we can find solutions for other affinely related profiles. For example, the NACA profiles designated by 8405, 8410, 8415 all have the same distribution, same nose radius etc.; only the absolute magnitude of t/c is different. This rule can be extended to transonic flow range also. From Figure 9.13, it is seen that in the transonic range, the aerodynamic coefficients change very quickly with Mach number, so that the proper values to be considered are not Mx, CL, CD and Cp; instead they are x, CL, C D and Cp.

From the discussion made so far, we can make the following remarks:

1. For subsonic and supersonic flows, the governing equation (11 — M^ |) фхх + фгг = 0 is independent of y, so that the results from similarity rules can be applied to any gas; but for transonic flow, the potential equations are not independent of y. Therefore, the results have to be properly applied to different gases, with suitable correction for y, for example, a probe used for air in transonic range can be calibrated for steam.

2. For transonic flow:

t 2/3

c, ~ cL ~ (- )

c, ~ cL ~ (c )

Cp – CL

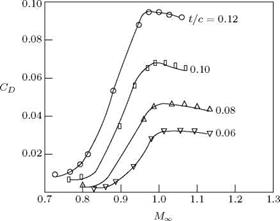
Transonic flow is characterized by the occurrence of shock and boundary layer separation. This explains the steep increase in CD at transonic range. We should also recall that the shock should be sufficiently weak for small perturbation. For circular cylinder this theory cannot be applied, because the perturbations are not small.