The Prandtl-Glauert Rule

This is only an approximation and a greater simplification compared to Gothert’s rule. Here we need not effect any transformation in the z-direction at all. That means Equation (9.118) is no more necessary. Only Equation (9.116) which gives transformation to planform alone is necessary.

General considerations

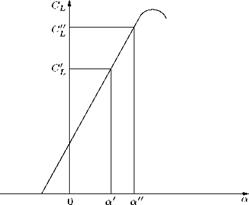
The P-G rule introduces the concept of affinely related profiles in incompressible flow. Affinely related profiles are those for which, for example, the t/c ratio alone is different and a and f are same, that is, all the ordinates of the two profiles are related simply by a constant.

Similarly, we can obtain affinely related profiles by changing a alone or f alone. In general, affinely related profiles as shown in Figure 9.17, can be obtained by:

We should effect only one of these parameters in Equation (9.122), in order to get affinely related profiles. For such profiles, it follows from theory and experiment that:

This can be thought as: if a for one wing is K times a for the second wing, then the CL, Cp and CM for the first wing should be correspondingly K times larger than those for the second wing. This is so because of the linearity of lift curve, shown in Figure 9.18.

These relationships hold only for the linear portion, because of the linearity involved in the theory.

Figure 9.18 Lift coefficient variation with angle of attack.

P-G Rule for Two-Dimensional Flow, using Equations (9.122) and (9.123)

We have to use Equation (9.122) with (9.118) and, (9.123) with (9.115), and set K = J11 — Ml | in Equations (9.122) and (9.123). What we have to prescribe now is our postulation for P-G rule versions I and II:

Version I:

MT = 0, for subsonic flow and, therefore,

t_ _ f _ a

t’ f a

where the prime refers to incompressible case. Version II:

MT = v/2 for supersonic flow and

t _
1 — Ml

Therefore,

C^_CpC±_ t 1 1

CP"C CP" Kl" ^jT-MT

where the double prime refers to transformed profile.

Application to Wings

The general relation between the pressure coefficients of closely related wing profiles [Equation (9.115)] is:

	1 1 – Mi

where “s” is the semi-span of wing. This transformed pressure coefficient ratio corresponds to Mi = 0 (Version I of P-G rule), for subsonic flow.

For Mi = V2 (supersonic flow), by Equation (9.125) of Version II, we get:

	1
(9.126)
1 – m^ I 1 1 – Ml
(9.127)

By Gothert rule [Equation (9.115)], we have:

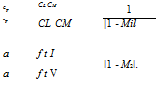(9.118)

By similarity rule for affinely related profiles in incompressible flow [Equation (9.122)], if:

t_ _ f_ _ <a_

t" f a"

then

c± = cl ер cl

CL = * cl 1

(9.123)

This is an empirical rule. For low speed flows, this can be explained with respect to a. But these equations are only approximate. Actually, for supersonic flow, CL does not depend on t at all. It depends only on f and a. We relate the given profile in compressible flow (unprimed) to the transformed profile (double primed) by:

t _ f _ a

t" f a"

With Equations (9.124a) and (9.118), we find that:

t’ t"
CL = 1 /11 – mi t t"
or *1	1 – Ml

Then the aerodynamic coefficients of the given profile in compressible flow are related to those of the transformed profile (which has the same geometry) in incompressible flow or at Ml = V2 by:

Cp _CL _ Cm _ 1

cp CL CM VIі – mi

because

C^ = c±Cl c c C" cp cp cp

1 1 – Ml

1 — Ml I by Equations (9.115) and (9.123).

Application to Wings of Finite Span

The Gothert’s rule [Equation (9.115)] states that:

1

|i – ML

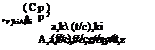and by P-G rule, we have:

1
(9.126a)
1 – ML
Equation (9.126a) is only an approximate relation. Further: (Cl) a, a,t/c, f/c (Cm ) A, a,t/c, f/c 1
(9.127a)
1 – Ml

The P-G rule is only approximate, but the Gothert’s rule, though exact, is very tedious, especially in three-dimensions, because here we have to transform the profile also. For P-G rule, only the planform has to be transformed.

From the P-G rule, for three-dimensional wings we obtain a similarity rule in the following way: if the relation:

CP = 6’Fi
(9.128)

for a wing is known at Ml = 0 and Ml = – Jl, then it follows for an arbitrary Mach number from Equations (9.116), (9.117) and (9.126), that:

Cp = L в. F2 ( X, A tan ф, Ах/11 — Ml |, c, Z

(9.129a) (9.1297>)

-.F^X, A tan ф, Ау/11 — Ml| ^ -,F^X, A tan ф, Аyj |1 — M2|^

1 – Ml

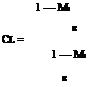where X is the taper ratio.

In Equation (9.129a): в means a or f/c or t/c.

In Equation (9.129Ь): в means a or f/c or t/c, but t/c only in subsonic flow. In Equation (9.129c): в means either t/c or f/c.

In Equations (9.128) and (9.129), ф is the angle of sweep for the wing.

Application to Bodies of Revolution

The application of P-G rule to bodies of revolution is similar to that for aerofoils (2-D), that is, no transformation of the body is necessary. The aerodynamic coefficients in compressible flow are the same as in incompressible flow or at Mx = V2. Hence, there is no Mach number effect at all and the results are same as those for slender body theory.

This contradicts the more exact Gothert rule. A closer examination shows that the P-G rule for bodies of revolution is valid only for very slender and extremely pointed (sharp-nosed) bodies. This theory is applied to rockets, very small aspect ratio wings, etc. Of course, wave drag is influenced by M even for slender bodies. We can use the results of incompressible flow for calculation of pressure distribution, etc.

From Figure 9.16(c), it is seen that for very small aspect ratio, the effect of Mach number is very small, and at A = 0 the Mach number effect vanishes.

9.17.6 The von Karman Rule for Transonic Flow Application to Wings For M, x) = 1:
Cp = e2/3F5(X, A tan ф, Ав1/3, x/c, y/s)	(9.130a)
CL = e2/3F6(X, A tan ф, Ae1/3)	(9.130i>)
CD = e5/3F7(X, A tan ф, Ae1/3).	(9.130c)

Mathematically, these can be derived from the nonlinear differential equation (9.49). These laws are also approximately valid in the vicinity of MOT = 1. The main advantage of these similarity rules is that we have to investigate the influence of X, A tan ф, Ав1/3 only and not the influence of X, A, ф and в separately, which is very tedious. Thus, the rules are very important for experimental investigations.

Application to Bodies of Revolution

The pressure distribution of a body (unprimed) is related to the pressure distribution of an affinely related body (primed) at MOT = 1, by the relation:

where the subscript f stands for fuselage. This rule was derived by von Karman, but later on it was shown that a correction factor should be applied.