MODEL ORDER REDUCTION FOR EVALUATIONS OF HQ
Inherently unstable/augmented aircraft systems are often highly augmented leading to very high-order dynamic systems (HODS) [47]. Mathematical description of aircraft and flight control system includes rigid and elastic body dynamics, actuator model, sensor models, and flight-control filters, and this would result in models of very high order. By LOTF approximation one can express the characteristics of an aircraft-control system in terms of flight mechanics models to appropriately evaluate the HQs. For this model, order reduction techniques for generation of equivalent LOTF are required. Generation of LOTF for analytical evaluation of HQs is a very important part of the overall FCS development process for a modern high – performance aircraft. The direct methods for evaluating HQs are piloted flight simulation and flight testing. The HQ criteria are often specified in terms of second-order TF constants with some additional parameters, such as time delay. Generation of LOTF with a specified structure and order becomes important for highly augmented aircraft. Because of increased control system integration, sophistication, and coupling, it becomes difficult to compute LOTF as additional modes are introduced in the region of pilot crossover.
There are several methods for obtaining LOTF models for HQ evaluation: (1) frequency response matching (amplitude and phase) over a selected range using numerical search routines, (2) system identification methods based on I/O data collected from flight tests and piloted simulation, and (3) balanced model reduction technique based on model decomposition of HOTF models in to high-, mid-, and low-bands and Hankel reduction of each of the three subsystems [6-8].
In the case of the frequency response matching technique, the cost normally used is
1 N
J = – V(AG/ + WDp2)
j=1
Here, N = number of discrete frequencies w,; AG is the amplitude difference, in decibels, between the actual (HOTF data) and (LOTF) model predicted response; AP is the phase difference in degrees; and W is the weighting factor, usually chosen as 0.018. The frequency range should be chosen to include the essential modes of the aircraft, the usual choice being 0.1-10 rad/s. For the frequency range, 20 points per
|
E-1 (Equation system bounds) E-1 (Equation system bounds)
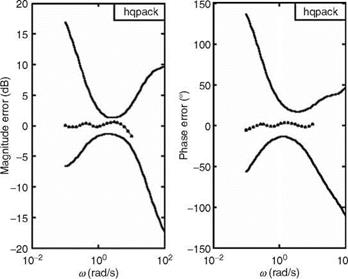
FIGURE 10.8 LOTF estimation error bounds for a configuration. (From Shaik, I., Evaluation of NLR handling qualities database for a large transport aircraft using HQPACK. Project Document FC 0519, National Aerospace Laboratories, Bangalore, December 2005. With permission.) |
decade can be used for model fitting. The structure of the LOTF model should be akin to the aircraft modes to be evaluated for HQ. Figure 10.8 shows error bounds obtained for fitting an LOTF to an HODS of a transport aircraft.