The Equations of Motion in the Extreme Ground Effect
11.1.1 Order Estimates and Assumptions
We turn to the evaluation of the form of the quintic equations of motion for h —> 0; see Rozhdestvensky [181]. In section 4, order estimates were obtained for the major aerodynamic coefficients on the basis of a mathematical model of a simple flying wing configuration in immediate proximity to the ground. In particular, for an adjusted angle of pitch (in radians) and a curvature of the wing sections of the order of 0(h),
Cyo, mzo= 0(1), CXiQ = 0(h). (11.25)
As per the previous analysis, the derivatives of the aerodynamic coefficients have the following order of magnitude:
(Cy, mz)h^ = 0(1), (11.26)
С’шё = o(i). (11.27)
Additionally, we assume that the viscous drag of the configuration does not vary with a small variation in the ground clearance and the pitch angle. To evaluate the order of magnitude of the coefficient Cf7, which represents the derivative of the thrust coefficient with respect to the relative speed, it is assumed that the drop of the thrust versus the cruise speed is linear, so that the (current) thrust T of the engines can be expressed in terms of the relative speed of motion, installed thrust Tm and cruise thrust T0 as
T = Tm-U(Tm – T0), £/ = yp (11.28)
b’o
where U0 is the design cruise speed. Introducing the thrust coefficient as
2T 2Tm U 2(Tm — T0)
‘ pUfS pUiS U0 рСуаЩв ’
wherefrom the derivative of the thrust coefficient with respect to the relative speed is given by
s-iU _ 2(Tm — T0) _ 2Cyo(Tm — T0) _ /Tm To
* “ PU*S ~ pCyoU*S – yovw w)
= -Cyo (cTm -^-)=CX – CyoCTm, (11.29)
where Crm = Tm/W is the installed thrust-to-weight ratio that characterizes the relative power capacity of the vehicle.
Recalling previous order estimates and assuming additionally that the installed thrust-to-weight ratio Crm = 0(h),
c? =Cx-CyoCTm=0(h). (11.30)
It seems rational to consider the magnitude of yt as that of the order of O(h). In other words, the ordinate of the thrust line is assumed comparable with the ground clearance.
Another convention to be adopted is related to the density factor p that enters the equations of motion. Based on the statistics for existing and projected wing-in-ground-effect craft (see Rozhdestvensky [182]) we can assume that the product of the vehicle’s density and relative ground clearance is of the order of 0(1). In this case, it is appropriate to introduce, instead of /z, a new quantity p^ = p h = 0(1), which can be called the reduced density.
11.1.2 Asymptotic Form of the Equations of Motion for h —ї 0
Employing these estimates and conventions about the orders of magnitude (in terms of h) and neglecting terms of the order 0(h) and higher, we can reduce the equations (11.18)—(11.20) to
Mh^-=0, (11.31)
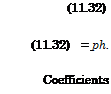 d2h – і ~ ~
d2h – і ~ ~
Ph ^2 — al h ~h h ~b G-з в – f – 0-4
d20 ^
Ph iz ~^2 — h T b2 h + Ьз в + 65 #,
where ai = hCy, a2 = hCy, a3 = hC^, a4 = hCy, and ph bi (i = 1,2,3,4) are given by the formulas
61 = hmj, b2 = hmhz, 63 = hmGz, 64 = hm9z.
Note that coefficients ai and bi are of the order of unity, because for each of the above derivatives,
coefficient^’^ = O^-j.
![]() The system of equations (11.32) and (11.33) has a structure similar to that of equations (11.9) and (11.10), derived on the basis of Irodov’s assumption
The system of equations (11.32) and (11.33) has a structure similar to that of equations (11.9) and (11.10), derived on the basis of Irodov’s assumption
of no perturbation in speed. It gives birth to a quartic characteristic equa
tion (11.11) whose coefficients are identical to А*, і = 1… 4, though written somewhat differently:
A =———- т(Ьа ~b iz ^2)? (11.35)
A2 =—————————– ^“7“ [&4 b2 – a2 64 + flh (63 + izdi)], (11.36)
lz
As = —2^(a2 — CL4 b — as b2), (11.37)
Mh lz
A4 = -^r-(ai b3 – a3 6i). (11.38)
Mh lz
The advantage of the formulation presented above consists of the reduction in the number of parameters on which Ai depend. In particular, for h —> 0, the relative clearance h does not enter the coefficients of the quartic equation explicitly. Thus, the coefficients of the quartic depend (nonlinearly) only on the reduced density цh and ratios є/h that characterize the design geometrical and kinematic parameters of the vehicle. The parameter є = О(h) can be the adjusted angle of pitch в or the maximum curvature c of the lower surface of the wing related to /г, etc.
The variation of speed can be analyzed by introducing “large time” t = 0(1 /К) and “very large time” t = 0(1 /h2). It can be shown that on the scale of a “large time,” the variation of the speed of the vehicle is mostly driven by perturbations in height and pitch, whereas on the scale of “very large time” the variation of speed is determined by the perturbation of speed proper. In the latter case, the perturbed equation for speed is completely uncoupled from those for height and pitch and has the form
![]() = -2CX)U’,
= -2CX)U’,
where t2 = h2 t is a “squeezed” time variable and /h and Cx = Cx/h
are quantities of the order of unity.











