Bernolli’s/Continuity Equations
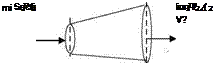
The continuity equation relates density, velocity, and area at one section of the flow to the same quantities at another section. In Figure A2, the flow is shown to be bounded by two streamlines. The mass flow rates at section 1 and 2 are given by [3]
m 1 = pjAr V and m2 = P2.A2V2
Since mass can neither be created nor destroyed,
m 1 = m 2 or p1A1V = p2A2V2
This is the continuity equation for steady flow.
 |
Another popular equation that relates pressure and velocity at one point in the flow to another point is the Bernoulli’s equation. It essentially follows from the Newton’s second law, which states that
I
![]()
![]()
![]()
![]()
 FIGURE A3 Forces on a fluid element for developing Bernoulli’s equation.
FIGURE A3 Forces on a fluid element for developing Bernoulli’s equation.
Force = mass x acceleration
In Figure A3, if P is the pressure on top of the fluid element (shown by a cuboid), the net force is given by
F = P dx dy — P + — dz dx dy
or
F = — (dx dy dz) dz
Since mass is density multiplied by volume
m = p(dx dy dz)
Also, along the z-axis, acceleration is given by the rate of change of velocity
dV _ dV dz _ dV dt dz dt dz
From Newton’s second law
F = ma
Substituting for F and a from the above, we have
dP dV
F = — (dx dy dz) = p(dx dy dz) V
dz dz
or
This equation is called the momentum equation for steady, inviscid flow. Considering point 1 with quantities p and V and point 2 with P2 and V2 in a flow, the momentum equation can be integrated to yield
1 2 1 2
P1 + 2 pv = P2 + 2 pv| (A-16)
This is called the Beroulli’s equation for inviscid incompressible flows with gravity terms neglected. As speed increases, compressibility effects need to be accounted for and density can no longer be assumed constant. Bernoulli’s equation for compressible flows with gravity terms included is given by [1]
g P 1 2
———— V – V2 + gz = constant (A. 17)
g – 1 P 2
where g is the acceleration due to gravity.











