The Normal Shock Relations for a Perfect Gas

For a calorically perfect gas, we have the equation of state, viz.

p = pRT

and the enthalpy is given by:

h = cpT.

Equations (9.133) – (9.137) form a set of five equations with five unknowns: p2, p2, T2, V2 and h2. Hence, they can be solved algebraically. Inotherwords, Equations (9.133)-(9.135) are the general equations for a

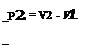normal shock wave and for a perfect gas, it is possible to obtain explicit solutions in terms of Mach number, M, ahead of the shock using Equations (9.136) and (9.137) along with Equations (9.133)-(9.135), as follows: Dividing Equation (9.134) by Equation (9.133), we get:

Recalling that the speed of sound a = vYPTP, Equation (9.138) becomes:

Now, a2 and a2 in Equation (9.139) may be replaced with energy equation for a perfect gas as follows. By energy equation, we have:

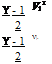From the above relation, a12 and a22 can be expressed as:

Because the flow process across the shock wave is adiabatic, a* in the above relations for af and a2 has the same constant value.

Substituting these relations into Equation (9.139), we get:

Dividing this equation by (V2 – Vj), we obtain:

Y + 1 2 Y – 1

———- a ———– — 1

2yV1 V2 2y

This may be solved to result in:

(9.140)

which is called the Prandtl relation.

In terms of the speed ratio M* = V/a*, Equation (9.140) can be expressed as:

Equation (9.141) implies that the velocity change across a normal shock must be from supersonic to subsonic and vice versa. But, it will be shown later in this section that only the former is possible. Hence, the Mach number behind a normal shock is always subsonic. This is a general result, not limited just to a calorically perfect gas.

The relation between the characteristic Mach number M* and actual Mach number M is given [Equation (2.25) of Rathakrishnan (2010) [1]] as:

Using Equation (9.142) to replace M* and M* in Equation (9.141), we get:

Equation (9.143) shows that, for a perfect gas, the Mach number behind the shock is a function of only the Mach number M1 ahead of the shock. It also shows that when M1 = 1, M2 = 1. This is the case of an infinitely weak normal shock, which is identical to a Mach wave. It is essential to realize that the Mach waves in a supersonic flow field are at an angle p, = sin-1 (1/M), which is always less than n/2. In other words, a Mach wave is essentially an isentropic wave degenerated to a level that the flow across it will not experience any significant change of property. But, as Mi increases above 1, the normal shock becomes stronger and M2 becomes progressively less than 1, and in the limit, as M1 ^<X), M2 approaches a finite minimum value, M2 ^ V(Y — 1)/2y, which for air (at standard conditions), with y = 14 is 0’378.

The ratio of velocities may also be written as:

V1 _ V22 _ V22

V = vv = a*1

Equations (9.142) and (9.144) are useful for the derivation of other normal shock relations. From Equation (9.133), we can write:

To obtain pressure relation, consider the momentum Equation (9.134):

P2 – P1 = P1V12 – P2V22

which, combined with Equation (9.133), gives:

P2 – P1 = P1 V1 (V1 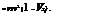– V2)

V2

Dividing throughout by p1, we get:

Now, recalling a = (yp1)/p1, we obtain:

= M (■ – V)•

Substituting for V2/V1 from Equation (9.145), we get:

Equation (9.147) may also be written as:

The ratio (p2 — pi) /p1 = Ap/pi is called the shock strength.

The state equation p = pRT can be used to get the temperature ratio. With the state equation, we can write:

T2 = f pi f pi T1 I pw IP2

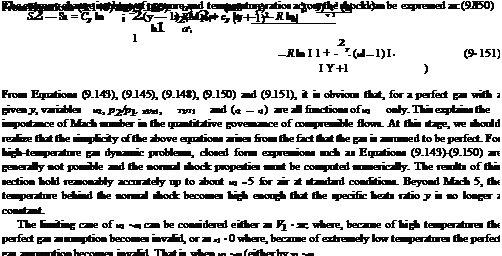Substituting Equations (9.148) and (9.145) into Equation (9.149) and rearranging, we get:

or by a ^ 0), the perfect gas assumption is not valid. But, it is interesting to examine the variation of properties across the normal shock, for this limiting case. When M1 ^ ж, we find, for y = 1.4:

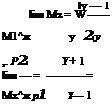= 0.378

6 P2

lim — = ж

M1^<x> p1

T2

lim — = ж.

М1^ж T1

At the other extreme case of an infinitely weak normal shock degenerating into a Mach wave, that is, at M1 = 1, Equations (9.143), (9.145), (9.148) and (9.150) yield M2 = p2/p1 = p2/p1 = T2/T1 = 1.That is, when Mi = 1, no finite changes occur across the wave.

Equation (9.151) justifies the statement we made earlier in this section: “from Prandtl equation, al­though it is possible for the flow to decelerate from supersonic to subsonic and vice versa across a normal shock wave, only the former is physically feasible.” From Equation (9.151), if M1 = 1, then As = 0; if M1 < 1, As < 0; and if M1 > 1, As > 0. Therefore, since it is necessary that As > 0 for a physically possible process, from the second law of thermodynamics, M1 must be greater than or equal to 1. When M1 is subsonic, the entropy across the wave decreases, which is impossible. Therefore, the only physi­cally possible flow is M1 > 1, and from the above results we have M2 < 1, p2/p1 > 1, p2/p1 > 1 and T2/T1 > 1.

The changes in flow properties across the shock take place within a very short distance, of the order of 10—5 cm. Hence, the velocity and temperature gradients inside the shock structure are very large. These large gradients result in increase of entropy across the shock. Also, these gradients internal to the shock provide heat conduction and viscous dissipation that render the shock process internally irreversible.