Oblique Shock Relations

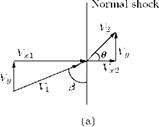
The flow through an oblique shock is illustrated in Figure 9.25(b). The flow through a normal shock (Figure 9.24(a)) has been modified to result in flow through an oblique shock, by superimposing a uniform velocity Vy (parallel to the normal shock) on the flow field of the normal shock (Figure 9.25(a)).

The resultant velocity upstream of the shock is V1 = Vx1 + Vy2 and is inclined at an angle в =

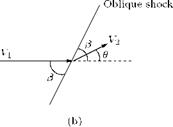tan-1(Vx1/Vy) to the shock. This angle в is called shock angle. The velocity component Vx2 is always less than Vx1; therefore, the inclination of the flow ahead of the shock and after the shock are different. The inclination ahead is always more than that behind the shock wave, that is, the flow is turned suddenly at the shock. Because Vx1 is always more than Vx2, the turning of the flow is always towards the shock. The angle в by which the flow turns towards the shock is called flow deflection angle and is positive as shown in Figure 9.25. The rotation of the flow field in Figure 9.25(a) by an angle в results in the field shown in Figure 9.25(b), with V1 in the horizontal direction. The shock in that field inclined at an angle в to the incoming supersonic flow is called the oblique shock.

Figure 9.25 Flow through an oblique shock wave.

The relations between the flow parameters upstream and downstream of the flow field through the oblique shock, illustrated in Figure 9.25(b), can be obtained from the normal shock relations, since the superposition of uniform velocity Vy on the normal shock flow field in Figure 9.25(a) does not affect the flow parameters (e. g., static pressure) defined for normal shock. The only change is that in the present case the upstream Mach number is:

^ Resultant velocity V1

Speed of sound a1

The component of the upstream Mach number M1 normal to the shock wave is:

Mn1 = M1 sin ft.

Thus, replacement of M1 with M1 sin в in normal shock relations given by Equations (9.145), (9.148), (9.150) and (9.151) results in the following relations for an oblique shock:

(y + 1) M2 sin2 в (y – 1)M2 sin2 в + 2

(9.159)

The normal component of Mach number behind the shock Mn2 is given by:

From the geometry of the oblique shock flow field shown in Figure 9.25, it is seen that the Mach number behind the oblique shock, M2, is related to Mn2 by:

In the above equations, M2 = V2/a2 and Mn2 = Vx2/a2. The Mach number M2 after a shock can be

obtained by combining Equations (9.160) and (9.161).

Numerical values of the oblique shock relations for a perfect gas, with y = 1.4, are presented in graphical form. The same in tabular form is given in Table 3 of the Appendix of Rathakrishnan (2010) [1].

It is seen from the oblique shock relations given by Equations (9.155)-(9.159) that the ratio of ther­modynamic variables depends only on the normal component of velocity (M1 sin в) ahead of the shock.

But, from normal shock analysis we know that this component must be supersonic, that is, Mi sin в > 1. This requirement imposes the restriction on the wave angle в that it cannot go below a limiting minimum value for any given M1. At this minimum limiting value of shock angle, the shock gets degenerated to an isentropic wave (also called Mach wave) across which the change of flow properties become negligibly small. Such a weak isentropic wave is termed Mach wave. The maximum value of в is that for a normal shock, в = n/2. Thus for a given initial Mach number M1, the possible range of wave angle is:

(9.162)

The limiting values of the wave angle in Equation (9.162) are of special significance. The limiting minimum value is sin-1 (M.) is the Mach angle x and the maximum value | corresponds to normal shock. Thus, the strongest wave possible in a given supersonic flow is the normal shock corresponding to the given M1. The weakest wave is the Mach wave corresponding to the given M1. It is essential to note that the shock wave formation is not mandatory in a supersonic flow. For example, in uniform supersonic streams such as the flow in a supersonic wind tunnel test-section, no shocks are formed when the test-section is empty, whereas the weakest limiting isentropic waves, namely the Mach waves, are always present in all supersonic flows. Even in the empty test-section of a supersonic tunnel the Mach waves are present. But we know that the waves in a supersonic flow are due to perturbations in the flow field. Therefore, it is natural to ask, “in an undisturbed uniform supersonic flow why should there be Mach waves present?” The answer to this question is the following. In a uniform supersonic flow such as that in a wind tunnel test-section, if the test-section walls are absolutely smooth there will not be any Mach wave present in the flow. However, absolute smooth surface is only a theoretical assumption. For instance, even surfaces such as that of a good quality Schlieren mirror has a finish of only about X/20, where X is the wavelength of light. Thus, any practical surface is with some roughness and not absolutely smooth. Therefore, any supersonic flow field generated by a practical device is bound to possess Mach waves. Indeed, the size of the gas molecules are enough to cause Mach wave generation. Therefore, even in a free supersonic flow without any solid confinement Mach waves will be present.

An important feature to be inferred here is that the Mach waves, like characteristics will be running to the left and right in the flow field. Because of this the Mach waves of opposite families prevailing in the flow field cross each other. But being the weakest degeneration of waves, the Mach waves would continue to propagate as linear waves even after passing through a number of Mach waves. In other words, the Mach waves would continue to be simple waves even after intersecting other Mach waves. Because of this nature of the Mach waves, a flow region traversed by the Mach waves is simple throughout.