Theoretical Prediction of Supersonic Transition

ALT is predicted by the Pfenningcr/Poll criterion [380).(3811 which is assumed to be valid at su­personic speeds (Table 2). but confirmation at the Mach numbers of interest is missing. Means to avoid ALT can be transposed from subsonic knowledge. Additional investigations are still strongly appreciated: because it is still a big challenge to design and manufacture a subsonic lead­ing edge for high aerodynamic performance at cruise and take-off which avoids ALT and is able to control CF1 by suction.

ALT. Attachmcni Line Transition CF1: Cross Row Instability ALT: Pfenmnger / Poll criterion, as for subsonics CF1, TSI: + strongly 3D + coupling of CFI and TSI + temperature profile (cooling) ♦ higher mode instabilities (HMI) Required: + improved linearized theory Cc*’) + improved analysis (PSE, DNS) + accurate 3D<solution of undisturbed flow TSI: Totlmicn-Schlichting-lnstability HMI: Higher Mode Instabilities

Tabic 2: Transition Effects and Prediction

СП, TSI and HMI are predicted by stability analysis of the boundary-layer flow distur­bances.

Linearized theory ("eN") has matured and can be used routinely, even for supersonic investigations [382J. if cooled surfaces and HMI are respected. Linearized theory solves the flow equations by superposition of two parts (383):

• undisturbed flow.

• small disturbance of one disturbance mode.

(one frequency resp. one wave length at one inclination to the flow direction).

Because the disturbances arc small, linearisation is allowed Eventually, it is possible to dense a pure local disturbance equation formulation, where at one position the disturbance equations are solved only in normal position to the wall. Resulting is the local amplification rate for the selected disturbance mode at this position. Total amplification rate is achieved by the fol­lowing procedure:

First, search for a point of indifference, where amplification rate is zero. i. e. it changes from damping to amplification. Stoning from this point, follow a suited integration line (down­stream). c. g. a stream line (of the "inviscid" flow). Integrate along this (stream) line the local amplification rates for the selected disturbance mode (which may change from point to point, depending on the selected integration strategy). When writing the integrated amplification rate A in exponential form

A = e

N = /n(A) becomes the so called N-factor. So, the result of linearized theory is an amplification rate, but not the disturbance itself. Therefore, transition prediction requires a vali­dation by transition tests in order to calibrate a relevant amplification rate. This calibration may depend on the environment (free flight, wind tunnel, external disturbances like turbulence, noise; internal disturbances like roughness, waviness, surface vibrations). The often cited limit N-factor of about 10 is restricted to specific calculation methods (incl. the selected boundary – layer codes) and applications; (some people suggest, that 10 was only detected, because we have 10 fingers…)

By definition, linearized theory cannot calculate

• changes of the undisturbed flow introduced by the disturbances

• interferencies of different amplification modes

• sensitivity of transition to external or internal disturbances (so-called receptivity).

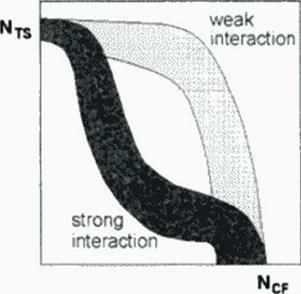
The limitations of linearized theory become increasingly obvious (Figure 110): More or less strong coupling of CFI and TSI may occur. The correlation figures for both cases arc completely different and. maybe, the whole zone in between can become valid. Additional effects like curvature and boundary layer divergence must be respected; hitherto especially the latter is not taken into account and may be responsible for some confusing results. Also, validity of linearized theory for CF1 is questioned (384). especially for strong CFI like on SCT-wings In supersonic flow, the TSI-waves are not normal to the flow direction, but inclined as nearly by the Mach angle. So coupling between TS1 and CFI may increase.

Figure 110 for Transition Prediction

Furthermore, linearized theory calculates only amplification rates (N-factors) which require validation by experiments, but ground test facilities for supersonic transition tests still do not exist.

A remedy is seen in Parabolized Stability Equations (PSE) (385) which arc able to han­dle coupling of CFI and TSI and – perhaps – to investigate the receptivity problem (386). (387). The latter must be solved to understand the supersonic wind tunnel simulation problem.

Analytical approaches were limited to very special problems.

For insight in the complicated flow physics and for calibration of the simplified meth­ods further investigations with Direct Numerical Simulation (DNS) – see e. g. (388) – is required.

For all engineering methods (linearized or parabolized disturbance theories) a prereq­uisite is the accurate solution of the undisturbed flow. It requires solution of the boundary layer profile for velocities and temperatures in both directions, accurate in the second derivatives. This is. for the years to come, the most severe task on strongly 3D flows.