A5 AXES (COORDINATES) TRANSFORMATIONS AND QUATERNIONS

The Euler angles C, U, f are the basic angles of the direction cosine matrix T required to transform a vector from earth to body axes. The relation between the Euler angles and angular rates is given by [8]

The matrix T of direction cosines to transform from earth to body axis is given by

	T11	T12	T13
T =	T21	T22	T23	(A.27)
	T31	T32	T33

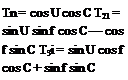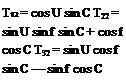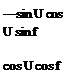where

The singularity encountered as pitch angle U approaches 90° can be avoided with the use of quaternions. The four components of quaternions are expressed in terms of Euler angles and to the body-axis angular rates as follows:

я1 = cos(C/2) cos(U/2) cos(f/2) + sin(C/2) sin(U/2) sin(f/2) я2 = cos(C/2) cos(U/2) sin(f/2) — sin(C/2) sin(U/2) cos(f/2) я3 = sin(C/2)cos(U/2) sin(f/2) + cos(C/2) sin(U/2) cos(f/2) я4 = sin(C/2)cos(U/2)cos(f/2) — cos(C/2) sin(U/2) sin(f/2)

(A.30)

These four components я1, я2, я3, я4 satisfy the constraint

a2 + a2 + a3 + a4 = 1 (A.31)

The elements of the transformation matrix T, in terms of the four components of quaternions, are given by

T11 = 2(я2 + я2) — 1 T12 = 2(я2Я3 + Я1Я4) T13 = 2(я2Я4 — Я1Я3)

T21 = 2(я2 Я3 — Я1Я4) T22 = 2(я2 + я|) — 1 T23 = 2(я3Я4 + Я1Я2) (A.32)

T31 = 2(я1 Я3 + Я2Я4) T32 = —2(я1Я2 + Я3 Я4) T33 = 2(я2 + я4) — 1

The Euler angles can be obtained from the quaternions as follows:

The sequence of rotation is important for accurate axes transformation. The first rotation is through angle C about the Z-axis, then through U about the Y-axis, and finally through angle f about the X-axis.