Relation between в and в

It is seen from Equation (9.161) that for determining M2 the flow deflection angle в must be known. Further, for each value of shock angle в at a given M1 there is a corresponding flow turning angle в. Therefore, в can also be expressed as a unique function of M1 and в. From Figure 9.25, we have:

Vx1

tan в =— (9.163)

Vy V

tan^ – в) = —. (9.164)

Vy

Combining Equations (9.163) and (9.164), we get:

tan^ – в) _ Vx2 VX1 .

Vx2 P_

Vx1 P2

Now, substituting for Pi/p2 from Equation (9.156), we get:

tan(^ — 9) (y — 1)Mj2 sin2 в + 2

tan в (y + 1)Mj sin2 в

Equation (9.166) is an implicit relation between 9 and в, for a given M1. With some trigonometric manipulation, this expression can be rewritten to show the dependence of 9 on Mach number Mj and shock angle в, as:

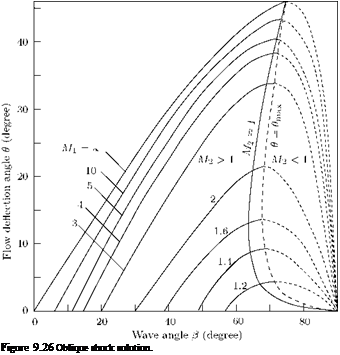Equation (9.167) is called the 9-в-M relation. This relation is important for the analysis of oblique shocks. The expression on the right-hand side of Equation (9.167) becomes zero at в = n/2 and в = sin-1 (M-), which are the limiting values of в, defined in Equation (9.162). The deflection angle 9 is positive in this range and must therefore have a maximum value. The results obtained from Equation (9.167) are plotted in Figure 9.26, for y = 1.4. From the plot of 9-в-M (Figure 9.26) curves, the following observations can be made:

Figure 9.27 Detached shocks.

1. For any given supersonic Mach number M1, there is a maximum value of в. Therefore, at a given M1, if в > emax, then no solution is possible for a straight oblique shock wave. In such cases, the shock will be curved and detached, as shown in Figure 9.27.

2. When в < emax, there are two possible solutions, for each value of в and M, having two different wave angles. The larger value of в is called the strong shock solution and the smaller value of в is referred to as the weak shock solution. For strong shock solution, the flow behind the shock becomes subsonic. For weak shock solution, the flow behind the oblique shock remains supersonic, except for a small range of в slightly smaller than emax, the zone bounded by the M2 = 1 curve and в = emax curve shown in Figure 9.26.

3. If в = 0, then в = n/2, giving rise to a normal shock, or в decreases to the limiting value g, that is, shock disappears and only Mach waves prevail in the flow field. That is, when the flow turning angle в is zero, the following two solutions are possible for the shock angle в, for a given M1. (a) Either в = n/2 giving rise to a normal shock which does not cause any flow deflection, but would decelerate the flow to subsonic level, or (b) в = sin—1 (1 /M1) = g corresponding a Mach wave, which even though inclined to the upstream flow, would not cause any flow deflection, being the limiting case of the weakest isentropic wave for a given M1.

A very useful form of в-в-M relation can be obtained by rearranging Equation (9.166) in the following manner: Dividing the numerator and denominator of the right-hand side of Equation (9.166) by 2M2 sin2 в and solving, we obtain:

Y + 1 tan (в — в) y — 1

Mj2 sin2 в 2 tan в

This can be simplified further to result in:

Y + 1 sin в sin в M2 sin2 в — 1 = M,2 .

1 в 2 1 cos (в — в)

For small deflection angles в, Equation (9.168) may be approximated as:

M2 sin2 в — 1 ^ M2 tan в] в.

If Mi is very large, then в ^ 1, but M1в » 1 and Equation (9.169) reduces to:

Y + 1

в = в.

It is important to note that oblique shocks are essentially compression fronts across which the flow decelerates and the static pressure, static temperature and static density jump to higher values. If the deceleration is such that the Mach number behind the shock continues to be greater than unity, the shock is termed weak oblique shock. If the downstream Mach number becomes less than unity then the shock is called strong oblique shock. It is essential to note that only weak oblique shocks are usually formed in any practical flow and it calls for special arrangement to generate strong oblique shocks. One such situation where strong oblique shocks are generated with special arrangements is the engine intakes of supersonic flight vehicles, where the engine has provision to control its backpressure. When the backpressure is increased to an appropriate value, the oblique shock at the engine inlet would become a strong shock and decelerate the supersonic flow passing through it to subsonic level.