Supersonic Flow over a Wedge

From studies on inviscid flows, we know that any streamline can be regarded as a solid boundary. In our present study, we treat the supersonic flow as inviscid and, therefore, here also the streamlines can be assumed as solid boundaries. Thus the oblique shock flow results, already described, can be used for solving practical problems like supersonic flow over a compression corner, as shown in Figure 9.28. For any given values of M1 and в, the values of M2 and в can be determined from oblique shock charts or table (oblique shock charts and table are given in the Appendix of Rathakrishnan (2010)).

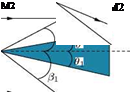
In a similar fashion, problems like supersonic flow over symmetrical and unsymmetrical wedges (Figure 9.29) and so on also can be solved with oblique shock relations, assuming the solid surfaces of the objects as streamlines in accordance with nonviscous (or inviscid) flow theory.

(b) Unsymmetrical wedge

Figure 9.29 Flow past (a) symmetrical and (b) unsymmetrical wedges.

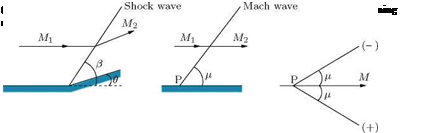
Figure 9.30 Waves in a supersonic stream.

In Figure 9.29(b), the flow on each side of the wedge is determined only by the inclination of the surface on that side. If the shocks are attached to the nose, the upper and lower surfaces are independent and there is no influence of wedge on the flow upstream of the shock waves.

In our discussion on shock angle в and flow turning angle в, we have seen that when в decreases to zero, в decreases to the limiting value p giving rise to Mach waves in the supersonic flow field (see Figure 9.30(b)), which is given from Equation (9.168) as:

M2 sin2 p – 1 = 0 (9.171)

Also, the pressure, temperature and density jump across the shock (p2 — pi, T2 — T1 and p2 — p{) given by Equations (9.156)-(9.158) become zero. There is, in fact, no finite disturbance in the flow. The point P in Figure 9.30(b) may be any point in the flow field. Then the angle p is simply a characteristic angle associated with the Mach number M by the relation:

(9.172)

This is called Mach angle-Mach number relation. These lines which may be drawn at any point in the flow field with inclination p are called Mach lines or Mach waves. It is essential to understand the difference between the Mach waves and Mach lines. Mach waves are the weakest isentropic waves in a supersonic flow field and the flow through them will experience only negligible changes of flow properties. Thus, a flow traversed by the Mach waves do not experience change of Mach number. Whereas the Mach lines, even though are weak isentropic waves will cause small but finite changes to the properties of a flow passing through them. In uniform supersonic flows, the Mach waves and Mach lines are linear and inclined at an angle given by p = sin-1 (1 /M). But in nonuniform supersonic flows the flow Mach number M varies from point to point and hence the Mach angle p, being a function of the flow Mach number, varies with M and the Mach lines are curved.

In the flow field at any point P (Figure 9.30(c)), there are always two lines which are inclined at angle p and intersect the streamline, as shown in Figure 9.30(c). In a three-dimensional flow, the Mach wave is in the form of a conical surface, with vertex at P. Thus, a two-dimensional flow of supersonic stream is always associated with two families of Mach lines. These are represented with plus and minus sign. In Figure 9.30(c), the Mach lines with ‘ + ’ sign run to the right of the streamline when viewed through the flow direction and those lines with “ — ” sign run to the left. These Mach lines which introduce an infinitesimal, but finite change to flow properties when a flow passes through them are also referred to

as characteristics, which are not physical unlike the Mach lines and Mach waves. But the mathematical concept of characteristics (taken as identical to the Mach lines), even though not physical forms the basis for the numerical method termed method of characteristics, used to design contoured nozzles to generate uniform and unidirectional supersonic flows.

At this stage it is essential to note the difference between the Mach waves, characteristics and expansion waves. Even though all these are isentropic waves, there is a distinct difference between them. Mach waves are weak isentropic waves across which the flow experiences insignificant change in its properties. Whereas, the expansion waves and characteristics are isentropic waves which introduce small, but finite property changes to a flow passing them. Thus, even though we loosely state that the Mach lines and Mach waves are isentropic waves in a supersonic flow, inclined at angle g to the freestream direction, in reality they are distinctly different. Mach waves are the weakest degeneration of isentropic waves to the limiting case of zero strength that a flow across which will not experience any change of property. Whereas, a Mach line is a weak isentropic wave in a supersonic flow field, causing small but finite change of properties to the flow passing through it.

The characteristic lines play an important role in the compression and expansion processes in the sense that it is only through these lines that it is possible to retard or accelerate a supersonic flow isentropically. Also, this concept will be employed in designing supersonic nozzles with Method of Characteristics.