Shock-Expansion Theory

The shock and expansion waves discussed in this chapter are the basis for analyzing large number of two-dimensional, supersonic flow problems by simply “patching” together appropriate combinations of two or more solutions. That is, the aerodynamic forces acting on a body present in a supersonic flow are governed by the shock and expansion waves formed at the surface of the body. This can be easily seen from the basic fact that the aerodynamic forces acting on a body depend on the pressure distribution around it and in supersonic flow, the pressure distribution over an object depends on the wave pattern on it, as shown in Figure 9.34.

Consider the two-dimensional diamond aerofoil kept at zero angle of attack in a uniform supersonic flow, as shown in Figure 9.34(a). The supersonic flow at Mj is first compressed and deflected through an angle e by the oblique shock wave at the leading edge, forcing the flow to travel parallel to the wedge surface. At the shoulder located at mid-chord, the flow is expanded through an angle 2e by the expansion fan. At the trailing edge, the flow is again deflected through an angle e, in order to bring it back to the original direction. Therefore, the surface pressures on the wedge segments ahead and after the shoulder, will be at a constant level over each segment for supersonic flow, according to oblique shock and the Prandtl-Meyer expansion theory.

On the diamond aerofoil, at zero angle of attack, the lift is zero because the pressure distributions on the top and bottom surfaces are the same. Therefore, the only aerodynamic force acting on the diamond

aerofoil is due to the higher-pressure on the forward face and lower-pressure on the rearward face. The drag per unit span is given by:

D = 2(p21 sin є – p31 sin є) = 2 (p2 – P3) (t/2)

that is:

Equation (9.182) gives an expression for drag experienced by a two-dimensional diamond aerofoil, kept at zero angle of attack in an inviscid flow. This is in contrast with the familiar result from studies on subsonic flow that, for two-dimensional inviscid flow over a wing of infinite span at a subsonic velocity, the drag force acting on the wing is zero – a theoretical result called d’Alembert’s paradox. In contrast with this, for supersonic flow, drag exists even in the idealized, nonviscous fluid. This new component of drag encountered when the flow is supersonic is called wave drag, and is fundamentally different from the skin-friction drag and separation drag which are associated with boundary layer in a viscous fluid. The wave drag is related to loss of total pressure and increase of entropy across the oblique shock waves generated by the aerofoil.

For the flat plate at an angle of attack a0 in a uniform supersonic flow, shown in Figure 9.34(c), from the uniform pressure on the top and bottom sides, the lift and drag are computed very easily, with the following equations:

L = p – pi) c cos ao D = (pi – pi) c sin ao,

where c is the chord.

Example 9.3

A flat plate is kept at 15° angle of attack to a Mach 2.4 air stream, as shown in Figure 9.35. Solve the flow field around the plate and determine the inclination of slipstream to the freestream direction using shock-expansion theory.

Solution

Using the shock and expansion wave properties, Table 9.1 can be formed.

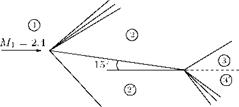Table 9.1 lists the flow properties around the flat plate. Slip-surface inclination relative to freestream is negligibly small. The velocity jump across the slip-surface is found to be 1 m/s.