Equation for the Streamlines from Kinematic Flow Condition

From Section 9.10, by kinematic flow condition we know that:

 

w/Vx

 

dz w

 

u

 

1 + — MX V

 

(1 — в2

 

wdx.

 

Vx dz

 

Substituting for u and w from Equation (9.198), we obtain:

 

Vxdz ^ 1 — y – (f’ + g) j = e(g’ — f’)dx Vxdz = e(g’ dx — f ‘dx) + e2(f ‘dz + g’dz) = в [ (g’dx + eg’dz) — (f’dx — ef ’dz) j = в (dg — df) ,

 

since:

 

df df df = dx + — dz = f dx — ^f dz dx dz dg dg. . dg = dx + -2 dz = gdx + вg dz. dx dz

 

Hence:

 

dz = — (dg — df). V

 

Integrating, we get the result:

This is the general solution of supersonic flow. Once the geometry is known, Equation (9.200) gives g and f and then from Equation (9.199) Cp and hence the lift and drag can be calculated. Therefore, in any problem if we are not interested in the geometry of the body present, then it is not necessary to find f and g. It is sufficient if f’ and g’ are found, to get the Cp, which is very much simpler.

Example 9.5

The upper and lower surfaces ofa symmetrical two-dimensional aerofoil are given by z = ±ex(1 — x/c)2, where c is the chord and e ^ 1. The aerofoil is at zero incidence in a steady supersonic stream of Mach number in positive x—direction. (a) Find the velocity components according to the linear theory in the upper region of disturbance. (b) Show that the drag coefficient of the aerofoil is given by:

8 e2

15 .

Solution

(a) Given:

Z = ±ex(1 — x/c)2.

The governing equation is:

2 д2ф д2ф

P dx2 — dZ2 =0
’(x, z) = f (x — Pz) for z > 0 (that is, above the aerofoil),

where P = JM^ — 1. On the upper surface, the boundary condition is:

(дФ L. ‘«- * (I)

With Equation (i), the boundary condition becomes:

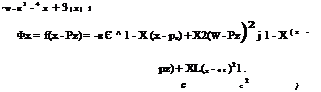Substituting X; in the equation for CD and simplifying, we get: