Existence of Characteristics in a Physical Problem

From the above discussions it is observed that:

0. Disturbances and Mach lines can be produced only by boundaries.

1. Disturbances can travel only in the downstream direction.

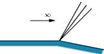
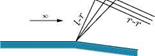
In Figure 9.39, we have shown that the characteristics of two families are independent of each other. This is because the geometries chosen are such that on one side of the boundary there is only one family of Mach lines. This is not the case always. In fact, in many situations of practical importance, the opposite characteristics will intersect each other as shown in Figure 9.40.

By knowing the type of Mach lines present in the problems, the equations can be suitably taken. From Equation (9.196), we have the potential function as:

ф(х, z) = f (x – Pz) + g(x + Pz),

where f represents the left-running Mach lines, on which g = 0 and g represents the right-running Mach lines, on which f = 0. The perturbation velocities are:

дф

u = = фх = f + g

дх

дф

w ф = e(g – f)

dz

Then the pressure coefficient is given by Equation (9.73a) as:

u 2

= -2 V = – VT(f + g°-