General Linear Solution for Supersonic Flow

The fundamental equation governing most of the compressible flow regime, within the frame of small perturbations is [Equation (9.52)]:

(1 – Игсо)фхх + Фzz = 0. (9.192)

Equation (9.192) is elliptic for < 1 and hyperbolic for > 1. There is hardly any method available for obtaining the analytical solution of the above equation for MOT < 1. But for MOT > 1, analytical solutions are available for Equation (9.192).

Solutions of Equation (9.192) for Mx > 1

For Mx > 1, Equation (9.192) is of the hyperbolic type, with the form being similar to that of the wave equation. The general solution to this equation can be written as the sum of two arbitrary functions f and g such that:

ф(х, z) = f (z — xtan j) + g(z + xtanj), (9.193)

where j is the Mach angle and:

(9.194)

The arbitrary functions f and g are to be determined from the boundary conditions for the specific problems.

Proof

To show that Equation (9.193) is the solution to Equation (9.192) when MOT > 1, rewrite Equation (9.193) as:

Ф = f (?) + g(n),

where? and n are the new variables, defined as:

? = z — x tan j, n = z + x tan j.

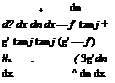Therefore,

On simplification this yields:

Фхх = tan2 x (f" + g")

dffd^ dg dn

дЁ, dz dn dz

фі = f’ + g’-

Differentiation of the above expression for фz with respect to z gives:

<Pzz = f" + g”. (9.195b)

Substituting Equations (9.195) into (9.192), we get:

(1 – MD tan2 x (f + g”) + (f" + g”) = 0.

This equation is satisfied for tan x from Equation (9.194). That is, Equation (9.193) is the general solution of Equation (9.192). However, the function f and g differ from problem to problem. Instead of Equation (9.193), solution to Equation (9.192) can also be written as:

Ф(х, z) = f (x – 0z) + g(x + 0z) (9.196)

where

в = cotx = J – 1. (9.197)

On inspection of the solution equation (9.193) or (9.196), it is seen that ф and hence, all the flow properties are constant along the straight lines given by the equation:

z = ± x tan x + constant.

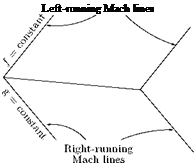
This equation gives two families of straight lines as shown in Figure 9.38, one family running to the left of the object and the other family running to the right, when viewed in the flow direction.

These are called Mach lines or characteristics. The lines of constant f that make a positive angle with the flow direction and run to the left of the disturbance (object) are called left-running characteristics and

Moo

Figure 9.39 Characteristics on different objects in supersonic flow.

lines of constant g, making a negative angle with the flow direction and running to the right of object are called right-running characteristics. Depending on the geometry of the object, there will only be left-running or right-running or both the characteristics present in the field as shown in Figure 9.39.