F-DISTRIBUTION AND F-TEST

For xj and x2, the normally distributed random variables with arbitrary means and variances as sj and s2, the following variances are defined:

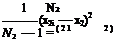1 N

N — 1Y1(xu — Xl)2 and -2

With sj and s2 the unbiased estimates of the variances, and x1; and x2i the samples from the Gaussian distribution, we have x2 = (N1s21)-1 and x2 = (N2s21)-2 as the x distributed variables with DOF h1 = N1 — 1 and h2 = N2 — 1. The ratio defined as F = (fy is described by F-distribution with (h1, h2) degrees of freedom.

The F-distribution is used in F-test, which provides a measure for the probability that the two independent samples of variables of sizes n1 and n2 have the same variance.

S2

The ratio t = -1 follows F-distribution with h1 and h2 DOF. The test hypotheses are

S2

formulated and tested for making decisions on the (unknown!) truth:

H1(s > s2): t > F1—„ H2(s2 < s2): t < Fa

at the level of 1 — a or a. The F-test is useful in determining a proper order or structure in