Gliding

For an aircraft gliding steadily with the engine off, as shown in Figure 10.6, the resultant aerodynamic force Fad balances the weight W, that is:

Fad – W = 0.

Thus, if L and D, respectively, are the lift and drag acting on the aircraft:

L = W cos у D = W sin y,

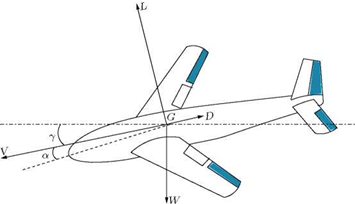where y is the angle which the direction of motion makes with the horizontal, called the gliding angle. Therefore:

This equation expresses the gliding angle у in terms of CL and CD. It should be noted that CL and CD here are the lift and drag coefficients for the whole aircraft. The attitude of the aircraft is the angle which a line fixed in the aircraft makes with the horizontal, as shown in Figure 10.6. If we measure the incidence a and attitude в from the same line we have в = а — у. Note that в and a can be negative, as shown in Figure 10.6, but the glide angle у is necessarily positive. Also note that the direction of the glide does not, in general, coincide with any fixed direction in the aircraft, in other words the attitude is a function of the incidence a.

The extreme attitude is that assumed when the aircraft is diving vertically, the terminal velocity dive. In this case the lift vanishes, the incidence is that of zero lift, and if the dive is undertaken from sufficiently great height, the weight just balances the drag, the speed being the terminal speed, may be five or six times the stalling speed. The attitude will then be about —90°.

Example 10.1

A glider of aspect ratio 6 has a drag polar of:

CD = 0.02 + 0.06CL.

Find the change in minimum angle of glide if the aspect ratio is increased to 10.

Solution

1 and 2 refer to aspect ratio 6 and 10, respectively.
1

6, Cd0 = 0.02, k = —— = 0.06.

ЛеДъ 1

wing efficiency is:

1

0.06 x n x 6 0.884.

For minimum glide angle, the drag should be minimum. For drag minimum, CDo = kC, therefore,

0.06Ci = 0.02

/__2 L1 у o._6

= 0.577.

For^?2 = 10:

_ 1 ne$t 2 _ 1 n x 0.884 x 10 = 0.036.

0.02 0.036 0.745.

The drag coefficients for aspect ratios 6 and 10 are:

CDl = 0.02 + 0.06 x 0.5772 = 0.04

CD2 = 0.02 + 0.036 x 0.7452 = 0.04.

Therefore, the gliding angles for these cases become:

Y1 = tan 1 |	‘ CDi j ,ClJ
= tan-1 (	ґ 0.04
ч0.577
= 3.966°
Y2 = tan-1 1	‘ 0.04
0.745

= 3.073°.

The difference between the gliding angles is:

Y1 – y2 = 3.966° – 3.073°