The Method of Characteristics

The one-dimensional continuity, momentum, and energy equations of a compress­ible, inviscid fluids are

dp dp du

dt 9x H 9x

9 u 9 u 1 9 p

+ u + — 0

dt dx p dx

9p 9p du

+ u + у p — 0. dt 9 x 9 x

This system of three equations supports three sets of characteristics. These characteristics may be found by combining the three equations in a special way. For this purpose, multiply (C1) by X and (C2) by в and add to (C3), where X and в are functions of the dependent variables p, u, and p.

Now X and в may be chosen such that all the derivatives of the dependent variables are in the form of a common convective derivative as follows:

— + V—. dt dx

There are three possible choices. They are

1. в — 0, X — – .

p

In this case, (C4) becomes

dp dp y p 9p 9p

+ u — + u — 0.

dt 9 x p dt 9 x,

Now, in the x-t plane, along the curve

dx

— u, dt

d — YP 0? = 0, (C7)

dt p at

where

d d dx d d d

dt dt + dt dX dt + U dX

along the P-characteristic. (C7) may be expressed in a differential form as follows:

dp — — dp = 0. (C8)

p

This may be integrated to yield

d( — ) = 0 or — = constant along a P-characteristic. (C9)

PV Pv

In other words, the flow is isentropic following the motion of a fluid element.

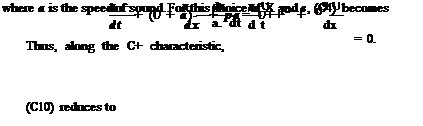2. X = 0, в = P (—^ = pa

d— dU

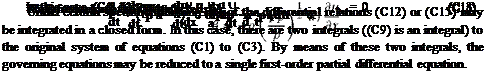— + p a— = 0 or dp + padu = 0. dt dt