Diffusion Equation

The dispersion-relation-preserving (DRP) scheme is well suited to compute numeri­cal solutions of diffusion equations. To illustrate this, consider computing the solution of the initial value problem governed by the heat equation as follows:

дU f д2U д2u

dt д X2 + д y2

at t = 0, u = f (x, y).

Before implementing the DRP scheme, it is advantageous to cast (D1) into a system of first-order equations. This may be done by introducing two auxiliary variables defined by

(D1) becomes

д U / д V д W дt дX^~ ду2

Now, the system of equations (D3) to (D5) is equivalent to (D1).

Upon applying the DRP scheme to (D3) to (D5), the finite difference system is

1 3 v(n) = — a U(n) Vl, m = Дх ajUl+j, m	(D6)
j=-3
13 W(n) = 1 a U(n) Wl, m = Ду ajUl, m+j y j=-3	(D7)
E(n) = K h a 1 v(n) i 1 w(n) lm =-3 aj AxVl+j, m + AyWlm+j	(D8)
3 u’,t=um+it c bjE’m j	(D9)
j=0

The time step At that can be used in (D9) is constrained by stability considera­tion. To determine the largest time step without triggering numerical instability, the first step is to find the dispersion relation of the system of finite difference equations (D6) to (D9). This is done by generalizing the discretized system to a set of finite difference equations with continuous variables and then take their Fourier-Laplace transforms. This leads to (a Ф will be used to denote the Fourier-Laplace transform of Ф ) the following:

v — iaU	(D10)
w — ів U	(D11)
Ё — K(iav + івії)	(D12)
— f(a^) p -і(&Н————- — Ё, 2n	(D13)

where f (a, в) is the Fourier transform of the initial condition f(x, y). a and в are the Fourier transform variables in the x and y directions, and ы is the Laplace transform variable. The solution of (D10) to (D13) is

і f (а, в)

U — 2 ♦

2п ы + ік (a2 + в )

The dispersion relation is given by setting the denominator of (D14) to zero, i. e.,

ы — – ік(а2 + в2). (D15)

Note that ы is purely imaginary for real a and в. According to the stability dia­gram of the DRP scheme (Figure 3.2) the stability limit along the negative imaginary axis of the rnAt plane is &At | < 0.29 . Thus, by dispersion relation (D15), in order to maintain numerical stability, it is required that

к(а2 + в2 )At < 0.29. (D16)

(D16) may be rewritten as

For the 7-point stencil DRP scheme, a Ax and в Ay are less than 1.75. Thus, by replacing a Ax and в Ay by 1.75 in (D17), the largest permissible time step, AtMax, is given by

It is a fact that diffusion current always flows outward from the source. Math­ematically speaking, this means that the solution at a point, away from the source depends only on the solution at points closer to the source. Therefore, at the bound­ary of a finite computation domain, the appropriate boundary treatment is to use backward difference stencils in the boundary region. There is no need to impose special boundary conditions.

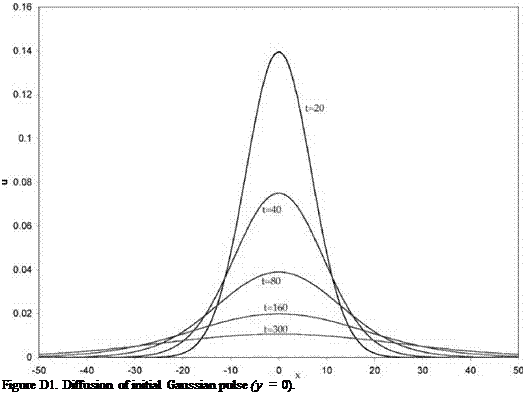
As a simple numerical example, consider the case of an initial Gaussian pulse,

i. e.,

where b is the half-width of the pulse. The exact solution is

Figure D1 shows the result of a computation using the 7-point stencil DRP scheme for the case b = 3. The length scale is Ax = Ay. The time scale is x^ . A 100 x 100 mesh was used in the computation. The numerical solutions at t = 20, 40, 80, 160, and 300 are displayed in the figure. The exact solution is shown by a dotted line. However, it cannot be easily seen because it differs from the numerical solution by less than the thickness of the lines of the figure. The numerical solution is extremely accurate.