A Flexible Wing — a Simple Theory of a PARAWIG
The so-called PARAWIG works as a sail wing in proximity to the ground. It is common knowledge that the main distinction of a sail compared to a rigid wing is that its surface is subject to deformation under the action of the flow, and the difference of the pressures on pressure and suction surfaces of the sail is proportional to its longitudinal curvature. According to Twaites[186], the problem of the aerodynamics of a sail consists of determining the flow for a given incidence в and excess of length S = ls — 1, where ls is the length of the sail.5 Essentially, this implies predicting the form of the sail wing, the aerodynamic loading and the tension on it. To solve for the flow, the conventional equation of the wing theory has to be supplemented by a condition of static equilibrium of each element. Naturally, the resulting system of equations is different from the traditional formulation for a rigid wing. One of the specific results of sail theory is the theoretical possibility of the existence of more than one form of sail for prescribed в and 5. However, there is no difficulty in choosing a real form. For such forms it turns out that the lift coefficient Cy of the sail exceeds Cy of the rigid wing approximately by the value of 0.636y/S. In what follows, we analyze very simple mathematical models of a PARAWIG in the concrete case of a flexible foil of infinite aspect ratio in the extreme ground effect. Fortunately, in this particular case, Twaites’s [186] verdict “…An analytical solution seems out of the question ” is not true. A complete linearized formulation for the perturbed velocity potential of a steady flow past a thin flexible foil near the ground can be written as
![]() d2<p dV
d2<p dV
dx2 dy2 ’ = y = h±0’ <12’46>
— = »-*• <12^
|?=0, у = 0 + 0, (12.48)
V(p —> 0, x2 + y2—> oo. (12.49)
Equation (12.47) accounts for the interaction of a flexible foil with the flow field and means that the pressure difference across the wing is proportional to the longitudinal curvature, and the factor of proportionality is the tension T.
![]() Again, all lengths are related to that of the chord.
Again, all lengths are related to that of the chord.
Applying the asymptotic approach advocated in this book for vanishingly small ground clearances /г —> 0, we can derive the following simplified formulation for a PARAWIG in a steady two-dimensional extreme ground effect flow:
![]() (12.50)
(12.50)
![]() d^ii = 1 f&y
d^ii = 1 f&y
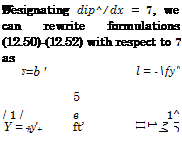 |
||
dx 2 dx2 ’
For a flexible wing, the ordinates у of the foil camber line with respect to the flat ground can be written as
y(x) = h + Ox + rj(x),
where 77 (x) represents the deformation of the wing due to the aerodynamic interaction with the flow, 77(0) = 77(1) = 0.
Integrating the first of the equations (12.53) and using the Kutta – Zhukovsky condition 7(0) = 0 for x = 0, y(0) = h, we obtain
Combining (12.54) with the second equation in (12.53), we obtain the following equation with respect to r/(x):
77" + a2r] = —6a2 x,
where
The solution of this equation was found in the form
rj = C cos ax + C2 sin ax — Ox.
Equations for determining the constants follow from the requirement that the deformation vanishes at the edges of the foil. Then,
?y(0) = Ci = 0, 77(1) = Ci cos a 4- C2 sin a — 9 = 0,
|
Finally, the deformation function rj(x) is obtained in form of the expression , 4 „/sinax , 4 rj(x) = в ————— x. 12.55 sin a / The excess length, which should be equal to J, can be calculated as Employing the smallness of 0 and, consequently, y’ = 0(0), x ; 1 #2 f1 ( 2cos2(ax) А i> s = is-i = – f fl2.2; ; -1) ae Л Jo sin (ax) / sin 2a > |
|
a* / sin 2a 1 2 ( -^ “I—- о— ) 2 sim a V 2a / J |
![]()
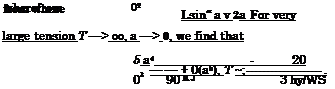 |
|
Cl = 0, c2
Now, we turn to calculation of the lift coefficient of a PARAWIG in the two dimensions and in very close proximity to the ground:
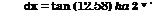 ~ о f1 /v о 0/sinax
~ о f1 /v о 0/sinax
Cy = 2 j(£)d£ = 2 tx+t[———————— x)
Jo Jo La a sin a )
For a small relative excess length, we can express the lift coefficient in terms of S —У 0, the angle of pitch, and the relative ground clearance h:
(12.59)
The relative effect of the flexibility of the foil can be evaluated by relating expression (12.58) for the lift coefficient of soft foil to that for a rigid foil (T = oo, a = 0). Eventually,
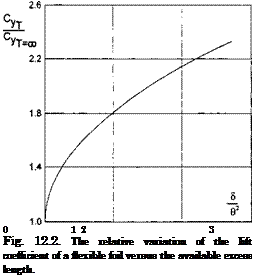
Figure 12.2 illustrates the relative variation of the lift coefficient of a flexible foil versus the combined parameter 5/в2.
 |
Essentially, the approach applied above suggests that the tension in the foil is sufficiently large Th = 0(1). It can be seen that at certain (eigen) combinations of the tension parameter and the relative ground clearance unstable modes occur of flow past a flexible lifting surface. Examining a homogeneous problem for deformations 77 of the foil,
r?" + a2T) = 0, ф) = 0, 77(1) = 0,
it is easy to conclude that the eigenvalues of the product Th are[78]
(Th)n = —Д-~, n = 1,2,…
By using the previous relationships, we can calculate the eigenvalues for the elongation 5 versus the form number n.
The corresponding eigen forms are described by expression
What are the relationships between the amplitude of a certain harmonic and the elongation parameter <5? Suppose that the amplitudes of the eigen forms of a foil are designated as rj0ri so that accounting for a — nn, the equation of the nth form becomes 77 = r]0ri sin7rnx. Then the elongation parameter S can be expressed as
5 = ls — 1 ~ ^ f (nnr]0ri)2 cos2 rmxdx = ^-‘K2n2riln,
2 Уо 4 n
so that for the nth harmonic, the amplitude will be related to the elongation 5 by
2V~5
The corresponding lift coefficient СУп will be
c-=ll sin”“di=^[ i-(-i)”i-
For even forms n = 2m(m = 1,2,…), the corresponding contribution СУп to the lift coefficient is zero.
For odd forms n = 2m — 1 (m = 1,2,…),
r = 4г?02т_х = 8л/б
У2т-1 7г/і(2ш — 1) /і7Г2(2ш — І)2 *
If we include all harmonics in the expression for the form of the foil, then,
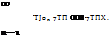
![]() oo
oo
v(x) = ХЖ sin тгпх,
 |
П— 1
where у = h + Ox + rj and rj(0) = rj( 1) = 0. In terms of the vortex strength 7 and foil ordinates у measured from the fiat ground surface, the set of governing equations becomes
![]() 5x(y7) = 5x’ 1 – (! -7)2 = – Ту", y = y{x).
5x(y7) = 5x’ 1 – (! -7)2 = – Ту", y = y{x).
Integration of the first equation of (12.63) and accounting for the Kutta – Zhukovsky condition 7(0) = 0 for x = 0, у = /г, gives
У
Substituting the previous result in the second equation of (12.63),
1 – % = – Ту".
yl
Multipying the latter equation by yf,
y’ – h2 = – Ty’y"
or and integrating, we obtain the expression
h? T., „
y+J = ~2y +C’
where C* is a constant to be determined later. Resolving with respect to y’,
2 z’ /i2>
or
|
/(C*-y-h?/yУ To determine the constant C* of integration we impose the conditions of no deformation at the edges of the wing, 2/(0) = h, y( 1) = в + h, wherefrom follows the equation for determining C* rh+0 |
|
у/C* — у — h2/y |
(12.64)
Introducing parameter a = у/2/Th, we can write (12.65) and (12.66) in alternative forms:
![]() x _ 1 fy___________ dy_______ o = f1+e______________ dу_________
x _ 1 fy___________ dy_______ o = f1+e______________ dу_________
aJi y/(C* – у – 1/y)’ Л /(C* – y-l/y)’
with ^ С* = С*//г, and 0 = 9/h.
The tension parameter T is defined by the condition of a prescribed elongation of the length of the foil:
(12.67) which together with equation (12.66) enables us to find the relationship between elongation and tension. Note that the slope of the foil contour yr in the equation for S has to be expressed through C* and y. The lift coefficient of a PARAWIG in the nonlinear case is determined by straightforward integration of the pressure jump across the foil:
cy= [ l{x)[2-~f{x)dx = -?[у'(1)-г/(0)] = (12.68)
Jo a
|
VC* – 2h |
|
C* – h – 9 – |
i. e., to the leading order the lift coefficient of a flexible foil is completely determined by the slopes of the foil contour at the edges. Performing calculations, we obtain
The notion of a flexible wing as a sail brings us to the consideration of an important property of a sail – porosity. Twaites [186] indicates that the lift – to-drag ratio for a sail is relatively small, partly due to porosity. Porosity is known to diminish the lift. The through flow due to porosity is assumed to be proportional to the pressure jump. For a porous flexible foil moving in immediate proximity to the ground, the governing equations have the form
where a(x) > 0 is a nondimensional porosity factor.
In the linearized 2-D case, the governing system (12.70) yields
Assuming a = const, and eliminating 7 from the previous expressions, we obtain the following ordinary differential equation with respect to the у ordinates of a porous flexible foil:
y’" + 2p" + ^V = 0. (12.72)
Representing у = h – f Ox – P T](x), where rj(0) = rj( 1) = 0, we can write the following equation with respect to the perturbation of the form of the foil
ф):
rl" + 2^t/’ + a? r{ = – а2в, a = a/h, a=y^- (12.73)
Although implicitly such a formulation implies that a = 0(h), it will be assumed that a is sufficiently small in comparion with the relative ground clearance. Investigation of eigen solutions of a homogeneous equation corresponding to (12.72) leads to the following expression for the relative speed of divergence:
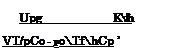 (12.74)
(12.74)
where da is a dimensional porosity factor and C0 is the chord of the foil. From observation of (12.74) we can conclude that the porosity of flexible foil entails a delay in the occurence of instability.
![]()
[1] This means that a cost-effective ocean-going vehicle capable of handling high seas should be sufficiently large. On the other hand, a vehicle of small dimensions is expected to be efficient on inland waters, where high seaworthiness is not required.
[2] This parameter represents the ratio of the distance of a wing from the ground to the chord of the wing and later on will be called the relative ground clearance.
[3] It can be shown that an infinite number of regular parameter expansions can be derived around h = oo, providing different ranges of validity with respect to h.
[4] E. Tuck seems to have been the first to introduce the term extreme ground effect, widely used in this book; see also Read [51].
[5] Extension to compressible flow will be considered in 5.1.
K. V. Rozhdestvensky, Aerodynamics of a Lifting System in Extreme Ground Effect © Springer-Verlag Berlin Heidelberg 2000
[6] In the steady case, this parameter coincides with the relative ground clearance h measured at the trailing edge.
[7] near the trailing edge /2,
[8] Here notation h stands for the characteristic relative ground clearance.
K. V. Rozhdestvensky, Aerodynamics of a Lifting System in Extreme Ground Effect © Springer-Verlag Berlin Heidelberg 2000
[10] For a wing with a straight trailing edge, xte = 0.
[11] Flow tangency conditions on the upper and lower surfaces of the wing:
[12] Parabolic arc
Let the foil have the form of a parabolic arc with relative curvature Sc. In this case, f(x) = 4x(l — x), a
[13] Strictly speaking, the theory of a wing of small aspect ratio implies that the local span increases monotonically in the downstream direction.
[14] With an asymptotic error of the order of 0(h).
[15] Note that the case under consideration corresponds to the order relationship 0 – C ol "C h – C 1, complying with the assumptions of linear theory: both the relative ground clearance and the angle of attack are small, and the latter is always smaller than the former.
[16] Coefficient of the moment around the leading edge:
[17] This conclusion correlates well with an exact solution of the problem of the optimal wing; see de Haller [134].
[18] To the order of 0[h, hln(l/h)}.
Note that in this formulation the ground clearance is measured from the trailing edge of the flap.
[20] As previously, this terminology implies that the maximum relative thickness is of the order of the relative ground clearance h. This assumption is practical and allows analyzing the influence of the thickness up to 10-15% of the chord.
[21] It may, for example, incorporate the factor of the contraction of the flow leaking from under the endplate.
[22] The assumption of the ideal fluid separation scheme on the flap is adequate for the power augmentation mode at rest. It can also be considered practically adequate for the cruise mode in a pronounced ground effect due to the domination of the channel flow contribution.
The “hats” are taken off.
[24] Energy equation
K. V. Rozhdestvensky, Aerodynamics of a Lifting System in Extreme Ground Effect © Springer-Verlag Berlin Heidelberg 2000
[25] If, for example, a wing in compressible flow has an angle of attack a, then the
angle of attack of the equivalent wing becomes a! — a/ y/l — Mq.
[27] Here instead of the notation for pitch 6, we use a.
[28] Far from the endplate on the lower surface of the wing (y —> —oo, у = 1—0),
[29] The ground clearance is measured between the hinge of the flap and the unperturbed position of the ground surface.
[30] Here, the reactive component of the lift coefficient is substracted from the total lift coefficient.
[31] i) It is common to assume that due to the very small ratio of densities of air and water, the surface under a lifting system in the ground effect behaves as if it were solid, ii) The assumption of stillness of the wavy boundary implies that the speeds of propagation of sea waves are small compared to the cruising speed of a wing-in-ground-effect vehicle. It is not difficult to introduce the effects of wave speed into the model.
[32] As earlier, all lengths are related to the root chord of the wing.
K. V. Rozhdestvensky, Aerodynamics of a Lifting System in Extreme Ground Effect © Springer-Verlag Berlin Heidelberg 2000
[33] For Lw = 2, the wave is two times longer than chord of the wing.
[34] The same is true for any wing with a flat lower surface moving in the extreme ground effect.
[35] Note that in the Appendix the longitudinal moment coeffcient mZw was also calculated around the trailing edge.
[36] Practically, this mode of motion takes place when the vehicle’s pitch is kept fixed
by controls.
[38] The minus derivative of the cruise lift coefficient with respect to the ground clearance can be interpreted as the “stiffness” of the spring in a simple massspring model of a vehicle on a dynamic aircushion.
[39] For large waves the height-to-wave ratio constitutes approximately 1/20.
[40] For a wing-in-ground-effect vehicle flying over the sea surface, this assumption is reasonable. It follows from the statistics of sea waves that the velocity of progressive waves does not exceed 1 knot, whereas the speed of existing and future wing-in-ground-effect vehicles varies in the range from 50 to 300 knots.
[41] Another argument exists in favor of this scheme based on some data showing that the magnitudes of drag, obtained in theory, are somewhat larger than the experimental ones.
[42] For the practical situation of blowing turbulent jets this result does not hold because due to certain momentum losses related to jet impingement upon the ground, the decrease in the averaged jet velocity and the entrainment of the surrounding air causes an increase in the jet width in the downstream direction.
[43] This case was considered by Gallington et al.
[44] As designated earlier, Л is the aspect ratio of the wing and 5ep is the characteristic relative gap under the endplates.
[45] Note that this and other quantities that may vary spanwise are assumed to be averaged in the lateral direction.
[46] In fact, the same rate of leakage from under the endplates allow for different combinations of the width of the effective gap under the endplates, the wing’s aspect ratio and the relative ground clearance.
[47] Based on a reentrant jet model.
[48] Most of the practical foil families have analytical descriptions.
[49] This is valid in a wide practical range of Strouhal numbers.
In the reentrant jet scheme the role of such a model parameter is played by the angle of inclination of the jet with respect to the downstream direction.
[51] This formula assumes that the wing is flat and the tips of the endplates are parallel to the ground.
[52] In the sense of minimal induced drag.
[53] The length of the plate is equal to that of the wing’s chord.
[54] Note that this formula does not include viscous pressure (form) drag and, consequently, gives a very approximate estimate of the viscous drag.
[55] That is, the lift coefficient, corresponding to the maximum aerodynamic efficiency.
[56] This can be achieved by using endplates with sharp tips or keels with sharp tips fixed on floats.
[57] That is to reduce the magnitude of the lift coefficient, corresponding to the maximum lift-to-drag ratio.
[58] The term was introduced by A. N. Panchenkov [64].
K. V. Rozhdestvensky, Aerodynamics of a Lifting System in Extreme Ground Effect © Springer-Verlag Berlin Heidelberg 2000
[60] The integrodifferential equation of the lifting line for an unbounded fluid can be found in Ashley and Landahl [161].
[61] C(z) is a ratio of local chord to the root chord.
[62] In Munk’s sense, i. e., ensuring minimal induced drag for a given lift.
[63] Note that for a parabolic planform, Л = 3//2.
[64] In the literature one may often encounter the alternative term ram in association with the ground effect.
[65] Note that for span-dominated and chord-dominated ground effects, the optimal planforms of the wings are different, although both give rise to a parabolic distribution of loading.
[66] If the lift coefficient is kept constant, while the wing approaches the ground, the induced drag coefficient decreases in both models of extreme ground effect.
Again, with the reference area equal to half that of the tandem.
[68] Matters of automatic control are covered in Diomidov [179].
[69] Incorporating both viscous and induced drag.
[70] This is valid for small relative distances of the wings of the tandem from the ground.
[71] All quantities and functions are rendered nondimensional by using the chord
length Co and the speed of forward motion U0.
K. V. Rozhdestvensky, Aerodynamics of a Lifting System in Extreme Ground Effect
© Springer-Verlag Berlin Heidelberg 2000
[75] In the case when the flutter is possible.
[76] It is possible to demonstrate that introduction of small porosity augments the speed of divergence; Efremov [71].
[77] Note that structural damping is not accounted for here.
[78] See also paragraph 12.2, dedicated to the approximate prediction of the occurrence of instability on an elastic foil under the action of tensile forces.











