The Phugoid Oscillation

Let an aircraft describing straight line phugoid, as shown in Figure 10.11, corresponding to C = 3/2, z = z1, cos в = 1, have its path slightly disturbed, say by a gust. It may then begin to describe a sinuous path of small slope, as in Figure 10.12, having the straight line as mean. This motion is called phugoid

oscillation. Since the vertical upward acceleration is — d2z/dt2, and since cos в = 1 to the first order, we have, for the vertical motion:

and therefore from Equation (10.10):

d2 z gz

dt2 Z1

This is simple harmonic motion whose period is 2n/(zi/g), showing that the disturbed motion is stable. In terms of the speed Vx the period is n-JlV^/g.

Example 10.3

An aircraft weighing 105600 N flies at an altitude where the air density is 0.16 kg/m3. The wing area, aspect ratio and efficiency are 28 m2, 6 and 0.95, respectively. If the drag polar is:

CD = 0.01 + kC2L,

determine the speed and Mach number at which the aerodynamic efficiency will be maximum.

Solution

Given, W = 105600 N, 5 = 28 m2, Ж = 6.

Therefore:

1

k = —– ~E>

nesR

_ 1

n x 0.95 x 6

= 0.05584.

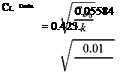For maximum aerodynamic efficiency, the drag has to be the minimum. For minimum drag, CD0 = kCL2 . Therefore, the lift coefficient becomes:

At level flight, L = W. The speed for drag minimum becomes:

UDmin =

Dmin

105600

x 0.16 x 28 x 0.423

From standard atmospheric table, for the altitude with density 0.16 kg/m3, the pressure is 11145.75 Pa. The corresponding speed of sound is:

a

1.4 11145.75

0. 16 = 312.3m/s.

The Mach number corresponding to minimum drag is:

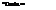UDn

a

333.84

312.3

Example 10.4

An aircraft of mass 30 000 kg, with an elliptical wing of area 225 m2, aspect ratio 7 delivering constant thrust of 53 kN, is taking off at sea level. The maximum possible lift coefficient is 2.0 and the profile drag coefficient while lift-off is 0.02 and the lift-off speed is 1.2 times the stalling speed. Assuming the rolling resistance to be negligible, calculate the lift-off distance required.

Solution

Given m = 30000 kg, S = 225 m2, T = 53000 N, CLmax = 2.0, CDf) = 0.02, A! = 7. The stalling speed Vs is the speed in level flight, with CLmax. Thus:

W

2 PSCl

30000 X 9.81

і x 1.225 x 225 x 2.0

32.68 m/s.

Therefore, the lift-off speed is:

V = 1.2 x Vs = 1.2 x 32.68 = 39.22 m/s.

The lift coefficient at lift-off becomes:

W

2 pV 2S mg

2 pV 2S

30000 x 9.81
2 x 1.225 x 39.222 x 225

1.388.

The drag coefficient at lift-off becomes:

1.3882 n x 1 x 7

= 0.108.

At lift-off, by force balance we have:

T – D 12

T – – pV2SCd T – ^ 1 x 1.225 x 225 x 0.108^ V2 T – 14.88 V2

We can write — as: dt

dV _dV ds _ ydV dt ds dt ds

where s is the distance along the run way, that is the distance travelled by the aircraft from starting to any instantaneous state. Therefore:

T – 14.88 V2 = mV—.

ds

This gives:

Integrating from s = 0 (V = 0) to s = slo (V = V), we have the lift-off distance as:

m

— ln. „

2 T – 14.88 V2

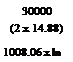
53000

53000 – (14.88 x 39.222) 53000

30111.46

10.10 Summary

For a flying machine, when the control surfaces are in their neutral positions the aircraft, like the aerofoil, has a median plane of symmetry, and when properly located the center of gravity G lies in this plane.

For an aircraft in straight level (horizontal) flight, the lift generated by the wings balances the weight and the thrust produced by the engine overcomes the drag.

Raising the elevators will decrease the lift on the tail, and will cause a pitching moment and moving the rudder will cause a yawing moment.

The ailerons move in opposite senses, one up, one down, by a single motion by the control column. If we depress the port aileron and therefore simultaneously raise the starboard one, the lift on the port wing will increase and that on the starboard wing will decrease so that the rolling moment will be caused tending to dip the starboard wing, and this sense will be positive. This movement also cause a yawing moment, for the drag on the two wings will likewise be altered.

When the aircraft velocity V is in a fixed straight line the flight is termed linear. When V is in the plane of symmetry the flight is termed symmetric. There are three types of linear symmetrical flight; gliding, horizontal, and climbing.

The flights can be steady (constant V) or accelerated. In the case of steady flight the resultant force on the aircraft must be zero. The forces are: (i) engine thrust, (ii) weight, (iii) aerodynamic force.

The lift coefficient CL is a function of the absolute angle of incidence a, and strongly influenced by the Reynolds number Re = pVl/g.

The stalled state is that in which the airflow on the suction side of the aerofoil is turbulent. Just before the stalled state sets in, the lift coefficient attains its maximum value, and the corresponding speed is called the stalling speed. Thus the stalling speed corresponds to a given CLmax. Stalling speed is a function of incidence.

For an aircraft gliding steadily with the engine off the resultant aerodynamic force Fad balances the weight W, that is:

Fad – W = 0.

Thus, if L and D, respectively, are the lift and drag acting on the aircraft:

L = W cos y D = W sin y,

where y is the angle which the direction of motion makes with the horizontal, called the gliding angle.

The forces acting on an aircraft in straight horizontal flight are the thrust T, weight W, and aerodynamic force Fad.

By proper choice of chord the incidence may be taken equal to the attitude and

L = W – T sin в D = T cos в.

In practice в is small, so that T = D, L = W, and

^ L W w

Cl = іpV2S = 2pV2S = 2pV2 ’

where w = W/S is called the wing loading, that is, the average load per unit area of wing plan. At the stalling speed VS, Cl becomes:

For aircraft flying steadily and horizontally, if Cl’ is the lift coefficient:

Cl'( 2 P^s) = W.

A sudden increase of incidence will increase the lift coefficient to:

cl( 2 pV’s)

and the aircraft will acquire an upward acceleration f given by:

c – clo( 2 pv 2 ^ = gf

so that it will begin to describe a curved path of radius of curvature r given by f = V2/r, where:

2W 1 _ 2w 1

SgP (,Cl – Cl’) ~ ~8P (Cl – Cl’) ‘

In this analysis we ignore the change in drag. If the speed is high, CL’ is small and CL cannot exceed CLmax for speed V. Thus the absolute minimum value of r is given by:

where VS is the appropriate stalling speed.

When an aircraft flying steadily and horizontally is rolled through an angle ф from the vertical, the lift will no longer balance the weight. If the aircraft is supposed to be flying towards us so that the starboard wing is dipped, the aircraft will accelerate in the direction of the resultant of L and W, and will continue to accelerate until a steady state is reached owing to the wind blowing across the body and producing a side force in the direction of the span. The direction of motion is now inclined to the plane of symmetry at an angle в, say, measured positively when the direction of motion is to starboard. The aircraft is now moving crab-wise in the straight path and is said to be sideslipping. If V is the speed, the component of V sin в perpendicular to the plane of symmetry is called the velocity of side-slip.

Side-slip will neither diminish the drag nor increase the lift as compared to symmetrical flight at the same speed.

A banked turn is a steady motion in a horizontal circle with the plane of symmetry inclined to the vertical. The direction of motion is longitudinal and there is no side-force.

A phugoid is the path of a particle which moves under gravity in a vertical plane and which is acted upon by a force L normal to the path and proportional to V2.

Exercise Problems

1. If the lift coefficient of an aircraft is given by:

CL = b sin

find the maximum value of the lift coefficient, for b = 2, a = 2n.

2.

Show that the minimum radius of a true banked turn, for a given angle of bank ф, is:

2w cosec ф gp CLmax

6. The aerodynamic efficiency of a sail plane of weight 3150 N and wing area 10 m2 is 30. If it is in level flight at sea level with a speed of 170 km/h, determine the drag coefficient.

[Answer: 0.0077]

7. An aircraft weighing 23000 N has a span of 14 m and average chord of 1.2 m. If it flies with a velocity of 90 m/s and angle of attack 4° in sea level (a) determine the lift curve slope. (b) If the aircraft glides steadily with the same speed at a glide angle of 6°, what will be the lift curve slope? (c) If the lift coefficient during glide has to be the same as that in the level flight what should be the flight speed?

[Answer: (a) 3.954, (b) 2.65, (c) 90.24 m/s]

8. An aircraft flies at a true speed of 350 m/s at an altitude where the pressure and temperature are 18.25 kPa and 216.5 K, respectively. (a) If a one-fourteenth scale model of the aircraft is to be tested, under dynamically similar conditions, in a wind tunnel with test-section temperature 288 K, what should be the pressure in the test-section? Assume the viscosity of air varies with temperature as T3/4 approximately. (b) Show that the forces on the model will be about 10% of the corresponding forces on the prototype.

[Answer: (a) 365.26 kPa]

9. An aircraft wing of span 10 m and mean chord 2 m is designed to develop 45 kN lift at freestream velocity 400 km/h and density 1.2 kg/m3. A 1/20 scale model of the wing section is tested in a wind tunnel at velocity 500 m/s and density 5.33 kg/m3. The total drag measured is 400 N. Assuming the wind tunnel data refer to a section of infinite span, calculate the total drag and aerodynamic efficiency of the aircraft wing, assuming the load distribution to be elliptic.

[Answer: D = 2.649 kN, L/D = 16.99]

[1] Conservation of matter (continuity equation).

• Newton’s second law (momentum equation).

[2]Note that in Equation (5.3) both V and ds are vector quantities. Therefore, their “dot” product has become §AB(U dx + vdy)

[3]From Equation (5.5), it is seen that the circulation is undefined for r < r0, that is, around the axis of rotation the circulation is not defined.

[4]The induced velocity for the circulation shown (that is, clockwise when viewed from right to left), is into the page. When the circulation direction is reversed (that is, counter clockwise) the induced velocity will be from the page to upwards.

[5]It would be of value to note that, for a steady, incompressible viscous flow, the Bernoulli equation can be applied between any two points along a streamline only. But for a steady, incompressible and inviscid (that is, potential) flow, the Bernoulli equation can be applied between any two points, in the entire flow field. That is, the two points between which the Bernoulli equation is applied need not lie on a streamline.

[6]2

KEi = 4 жруг.

Thus the total KE is:

KE = KE0 + 2KEi

[8] pco V 2

[9] RTx 00 ’

since by thermal state equation:

[10] Approximate the vortex sheet shown in Figure 7.4 by a series of straight panels.

• Let the vortex strength y(s) per unit length be constant over a given panel, but allow it to vary from one panel to the next.

• That is, the vortex strength per unit length of the n panels are Y1. Y2. Y3. ….. Yn. These panel strengths are unknowns. Therefore, the main objective of the vortex panel technique is to solve for Yj, j = 1 to n, such that the body surface becomes a streamline of the flow and the Kutta condition is also satisfied.

[11] We could use the source strength distribution to satisfy flow tangency and the vortex distribution to satisfy the Kutta condition.

[12] Results

[13] Calc. Induced Velocity and Pressure coeff. do 400 i=1,num

Vsurf(i) = Vinf*cos(alpha-phi(i)) do 410 j=1,num

if(j. ne. i)then

xcl = (xc(i)-xn(j))*cos(phi(j)) + (yc(i)-yn(j))*sin(phi(j)) ycl =-(xc(i)-xn(j))*sin(phi(j)) + (yc(i)-yn(j))*cos(phi(j)) beta= atan(xcl/ycl) – atan((xcl-s(j))/ycl) ulocal =

1 (1.0/(2.*pi))*(gamma(j)+(gamma(j+1)-gamma(j))*xcl/s(j))*beta

2 + (1.0/(2.*pi))

3 *ycl/s(j)*(gamma(j+1)-gamma(j))*log(r(i/j+1)/r(i/j)) vlocal =

(1.0/(2.*pi))*(gamma(j)+(gamma(j+1)-gamma(j))*xcl/s(j))

[14] Given the load distribution and the plan, find the profiles of the sections.

[15] Given the plan and the profiles, find the load distribution (that is the vorticity distribution).

[16]This assumption will fail at a stagnation point, for then v = V. However, this will not cause any subsequent difficulty.

[17]It is essential to note that Mach lines are weak isentropic waves across which the changes in the flow properties are small but finite, thus, Mach lines are different from the weak isentropic waves termed Mach waves across which the changes in the flow properties are negligible.