Plurality of Interpretations
An acoustic analogy may be useless if no simplification is made. In contrast when simplifications are accepted to take advantage from the formal simplicity of linear acoustics, the analogy cannot be exact anymore and becomes an interpretation. In some circumstances the same configuration can be interpreted differently, resorting to either Lighthill’s formalism or Ffowcs Williams & Hawkings’.
As an example consider the sketch of Fig. 4-(a) dealing with an excrescence attached to a plate of large dimensions, mimicking the side mirror of a car. Sound originates from the vicinity of the excrescence where intense vortex dynamics takes place. Lighthill’s interpretation formulates the problem with distributed quadrupoles Tj assumed to radiate in a medium limited by the surfaces of the plate and of the body. Boundary conditions need being specified all over the surfaces. The tensor Tj must be deduced from a simulation of the flow. Because the Mach number is small in the case of the side-mirror, the only affordable effort is often incompressible LES. This is not an issue when post-processing the flow field with Lighthill’s analogy, of course as long as there is no acoustic back-reaction on the flow. In principle the same configuration can be formulated with Ffowcs Williams & Hawkings’ analogy. The surfaces are not considered as boundary conditions anymore but as distributed additional dipoles radiating as if the medium was unbounded. These sources are essentially wall-pressure fluctuations if the Reynolds number of the flow is high enough, ensuring that inertial effects in the vortical motion dominate and that viscous terms may be neglected. The exact analogy states that the pressure includes the so-called hydrodynamic pressure associated with vorticity and the acoustic pressure associated with compressibility. If an incompressible simulation is used to feed the equation of the analogy with aerodynamic input data, the generation of sound by the surface is reproduced but the sound reflection by the surface is not. This is a significant source of error because the plate is larger than the acoustic wavelengths of interest. Furthermore sound radiates only in a half-space. In contrast, if accurate enough, a compressible simulation would account for the reflection.
|
Figure 4. Excrescence on a flat wall. Real configuration (a) and best-suited image representation (b). |
To cope with this issue, the problem can be stated by removing the plate and adding the symmetric images of both the flow and the excrescence (configuration (b)). The featured symmetric body is expectedly compact and now applying Ffowcs Williams & Hawkings’ analogy with an incompressible description of the flow as input data makes sense. In configuration (b) the dominant sources should be dipoles distributed over the surfaces because at low Mach number quadrupoles are much less efficient; this accepted property results from the higher cancellations between constitutive elements of a quadrupole. But precisely the symmetry of the equivalent flow induces partial cancellation of opposite wall-normal forces. This features quadrupoles which combine with Lighthill’s quadrupoles in the surrounding volume. In comparison the fluctuating forces parallel to the wall are doubled by the reflection. Again they are small at high Reynolds number, so that the quadrupole contribution can dominate, despite its intrinsic lower efficiency (Posson & Perrot (2006)). Introducing the image flow to account for the presence of a reflecting plane has been also discussed by Goldstein (1976) in connection with the noise generated by developed turbulent boundary layers over a flat plate. The net result is that, due to the cancellation of induced pressure forces, the sound remains fundamentally of quadrupole nature. Again the viscous forces parallel to the plate are generally ignored because they are negligible at high Reynolds number. A different situation can be encountered if the viscous forces are made much larger by wall roughness.
|
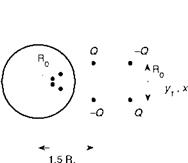
0 Figure 5. Academic exercise: scattering of a lateral quadrupole by a cylinder. Two-dimensional equivalent source distribution. |
The different ways of posing a problem of aeroacoustics are typically illustrated next on the example of the vortex-shedding sound from a circular cylinder in a flow (Fig.1-(a)). For simplicity, the mechanism is described in two dimensions and the incriminated vortex dynamics is reproduced by an equivalent lateral quadrupole close to the cylinder in the near wake, in accordance with Lighthill’s interpretation. The radiation process involves reflection or scattering of the quadrupole by the curved surface of the cylinder. At subsonic Mach numbers and in view of the vortex-shedding frequency f0 ~ 0.2Uq/D where U0 is the flow speed and D is the diameter, the region embedding the cylinder section and the quadrupole is of small extent compared to the acoustic wavelength. The wave equation or the Helmholtz equation becomes locally equivalent to Laplace’s equation. This means that the local acoustic motion can be assimilated to an incompressible potential flow. The sound field of a source close to the circle is obtained by removing the circle and adding two identical image sources : one at the center of the circle and the other one at distance R2/a, where a is the true distance of the source and R0 the circle radius. The resulting configuration is shown in Fig. 5, where the image sources at the center are not shown because they exactly cancel each other. The natural field that would be radiated by the isolated quadrupole in absence of the circle is shown in Fig. 6-(a), where the four expected lobes are clearly identified. Were the quadrupole close to a reflecting plane tangent to the circle, the field would be that of subplot (b), even less efficient. But the true sound as produced by the direct and image sources is much stronger and exhibits the two lobes of an equivalent dipole with orientation normal to the incident flow (subplot (c)). This is explained by the antisymmetric structure of the von Karman vortex street, from which the assumption of a lateral quadrupole is justified. Nearly the same sound field is obtained by just ignoring the direct sources (subplot (d)); the radiating efficiency is explained by the image sources only, in other words by the scattering. The dipole-like behavior is due to the different partial cancellations between the source pairs closest to and farthest from the center. The two-lobed pattern is what would be similarly predicted by the dominant, loading-noise term of Ffowcs Williams & Hawkings’ analogy. Indeed the dominant effect of vortex shedding is an oscillating induced lift on the cross-section of the rod, acting as a dipole. For this the equivalent source will be called a lift dipole. Both problem statements are found equivalent. Since the body is acoustically compact, the interpretation of Ffowcs Williams & Hawkings is better suited because it directly emphasizes the dipolar character of the sound field. Lighthill’s approach in this case shows that the quadrupole behavior of the source is dramatically modified by the reflection on the cylinder. This is because the circular section is a compact body and because the source is very close to it in terms of wavelengths. This fundamental change is more deeply discussed by Howe (2003) using the formalism of compact Green’s functions, not detailed here. It is worth noting that the case of the free-cylinder vortex shedding is very different from the side-mirror image flow. Changing from a symmetric to an antisymmetric flow pattern results in the excitation of a very efficient lift dipole.
Finally all classical statements of the acoustic analogy lead to the definition of equivalent moving sources in a linear wave equation. The sources can be monopoles, dipoles or quadrupoles. The formal solving of the wave equation and the effect of source motion on the radiated field are fundamental aspects, addressed in the next sections.