Discussion of Mathematical Models

In general, modeling of fluid motion is a complicated subject particularly with high speed turbulent flows. It is argued that simple models based on small disturbance potential flow equation, with boundary layer corrections are attractive, at least for educational purposes, to identify the difficulties of relevant phenomena at design conditions and to study successfully practical solutions for these problems.

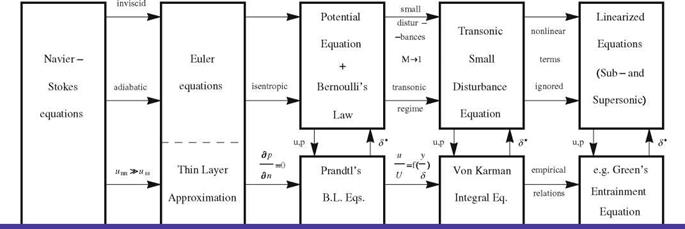
The students should be aware of the limitations of these simple models and the range of their validity. In the following chart, different formulations are listed with their relations, Fig. 1.5.

In the common commercial and military flight regimes, continuum mechanics assumptions are acceptable and the Navier-Stokes equations are considered the high fidelity model. For high Reynolds number flows, the viscous stresses and the heat conduction process are ignored outside a thin layer adjacent to the solid surfaces and in the wake.

Assuming inviscid and adiabatic flows, the Navier-Stokes equations reduce to the Euler equations, representing conservation of mass, momentum and energy for a perfect gas.

Far field: no disturbances (except 2—D)

irrotational

B. C. at solid surface: no slip, no penetration, temperature or heat transfer prescribed Fig. 1.5 From Navier-Stokes to linearized models

Adjacent to the solid surface, the thin layer approximation is based on ignoring the second order tangential derivatives in viscous and heat conduction terms, compared to the corresponding derivatives normal to the flow direction. Notice that the Euler equations are a subset of these equations. Therefore, outside a thin layer (its size depends on Reynolds number), all the viscous and heat conduction terms are ignored.

The Euler equations admit several modes, namely acoustic, entropy and vorticity modes (vorticity is twice the angular velocity of the fluid element around its center). For steady flows, with uniform upstream conditions, entropy is generated across shock waves, and for curved shocks, vorticity is generated due to variation of entropy from one streamline to another, according to a famous relation due to Crocco. At design conditions, shocks are usually assumed weak, hence isentropic conditions can be used. It follows then that vorticity vanishes. Irrotational flows are easier to handle since the fluid particles do not rotate around their centers as in rotational flows. With the assumption of zero vorticity, a potential function can be introduced (thanks to Stokes’ theorem), such that the velocity components are represented in terms of the partial derivatives of the potential function. Moreover, an integral of motion exists. For steady, isentropic, irrotational flows, the momentum equations can be integrated to give the most celebrated equation in fluid mechanics, namely Bernoulli’s law, which provides a relation for the pressure (or density) in terms of the velocity magnitude. Hence, the governing equations are reduced to one (nonlinear) equation for the potential function, in terms of one parameter, i. e. the free stream Mach number.

The steady potential flow solution (usually) does not satisfy the no slip boundary condition at a solid surface, since viscous effects are ignored, leading to zero skin friction drag (d’Alembert paradox). Prandtl introduced the boundary layer concept in 1904, to rectify these deficiencies. At least for attached flows over smooth streamlined thin bodies, the velocity in the boundary layer is almost tangent to the body surface, i. e. the velocity in the normal direction is small and its variation in this direction is also small, hence the pressure gradient normal to the wall is negligible.

Together with the thin layer approximation, boundary layer theory provides a pow­erful tool to fix the potential flow formulation, provided, of course, a viscous/inviscid interaction procedure is efficiently implemented. The boundary layer flow pushes up the flow outside the boundary layer and thus a pressure distribution different from the one without the boundary layer is established. This pressure distribution in return affects the boundary layer flow and the coupling is important to obtain the right interaction.

Both potential flow and Prandtl boundary layer models can be further simplified for thin bodies with attached flows. The full potential equation can be reduced to a small disturbance transonic equation, which is still nonlinear, and is able to model flows with both local subsonic and local supersonic regions separated by sonic line and possibly weak shocks. Assuming the flow profile inside the boundary layer, one can obtain a simplified formulation for the governing equations there following von Karman’s analysis. With these models, the coupling procedures are also simplified.

Finally, to obtain analytical solutions, at least for pure subsonic and pure super­sonic flows, the nonlinear small disturbance equation is linearized. Ignoring the

nonlinear terms can be justified away from the transonic regime. Superposition tech­niques can be used to establish solutions for realistic shapes. Also, empirical formulae can be used to solve the von Karman equation, in the boundary layer, for both laminar and turbulent flows.

In Fig. 1.5, the boundary conditions at the solid surface are the no slip and no penetration conditions for the velocity together with the specification of wall tem­perature or heat flux. In the far field, disturbances die out (except in some two dimensional cases).