Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
. Other Formulations
Then the irrotationality condition is identically satisfied, but substituting u and w into the conservation of mass results in
 |
 |
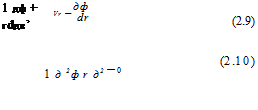In polar coordinates this is
This is the governing equation for potential flows, the Laplace equation. The perturbation velocity field is given by grad ф — , фф, (or in short notation
Vф). The boundary conditions become
VФ. П obstacle — (UІ + Vф).П obstacle — 0 (211)
Vф — 0 as x2 + z2 — ^ (2.11)
A streamfunction can be introduced: let ty(x, z) be the perturbation streamfunc – tion. The full stream function is & — Uz + ty(x, z). The perturbation velocity components are obtained from
|
дф дф u — , w — -д z д x |
(2.12) |
|
then the equation of conservation of mass is identically satisfied and substituting u and w in the irrotationality condition yields |
|
|
д2ф д2ф л* — d + a zt — 0 |
(2.13) |
|
In polar coordinates this is also |
|
|
1 дф дф Vr — r ~дв’ Ve — – d7 |
(2.14) |
|
д ( дф 1 д2ф dr Г dr + r дв2 0 |
(2.15) |
This is the governing equation for the streamfunction. The streamfunction also satisfies Laplace equation. The boundary conditions, however, read
& obstacle = (Uz + Ф) obstacle = const-
g■ – f) – 0 as x2 + z2 (2J6)
The first condition results from the identity V&.tobstacle — 0, where t represents a unit tangent vector to the solid surface (n. t — 0), which proves that & obstacie — const., the value of this constant is however not known a priori. The
Ф = const. lines are the streamlines of the flow. Solid obstacles are streamlines and conversely, streamlines can be materialized to represent a body surface.
When both, Ф and Ф exist, simultaneously, potential and stream functions are called conjugate harmonic functions. It can be easily shown that the curves Ф = const. are orthogonal to the curves Ф = const.
