Flow Past a Circular Cylinder

Finite bodies require that the sum of all sources and sinks be zero. Doublets, as limit of a source and a sink of equal and opposite intensity, have zero net volume flow. The superposition of a uniform flow and a doublet (D > 0) produces a flow field given by

cos в sin в

Vr = U cos в — D Ve = —U sin в — D — (2.29)

The velocity potential and streamfunction are

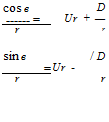
(2.30)

(2.31)

By inspection of the streamfunction, one can see that Ф = 0for r = a = UD. This solution represents the flow past a circular cylinder of radius a. At the surface of the cylinder, the tangency condition, Vr = 0, is satisfied. We have also seen earlier that the potential vortex admits streamlines which are circles centered at the origin. In fact, the most general solution of the flow past a circular cylinder of radius a is given by the superposition of the uniform flow, a doublet of intensity D = Ua2 and a potential vortex. The corresponding velocity field is

Note that the circulation Г is arbitrary. The tangency condition is satisfied by Vr(a, в) = 0. The asymptotic condition is also satisfied as V ^ Vro when r ^ro. Stagnation points are found on the cylinder by satisfying the condition

Г1

Ve(a, es) = -2U sines – = 0 (2.33)

2n a

This admits two solutions provided |Г| < 4nUa, namely es = arcsin (-4ra) and n + arcsin (4]fUa), where – П < es < П^. The stagnation points are points A and B in Fig. 2.9. The streamlines are given by

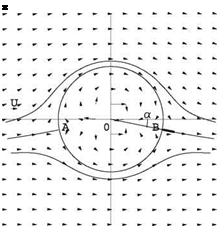Fig. 2.9 Flow past a circular cylinder with circulation

(2.34)

A remarkable streamline is the stagnation streamline, V = Гл. It is made of the cylinder and the two branches attached to the stagnation points.

The question of how to determine the value for Г is important. Within the inviscid flow framework, a possible mechanism for controlling the circulation is the use of a small flap, a thin flat plate placed perpendicular to the cylinder at es forcing the rear stagnation point to locate at point B, as shown in Fig. 2.9. Once the rear stagnation point is established, the front stagnation point A will settle at n – es. In a sense, es relates to the “incidence” a = —es of the cylinder. The previous equation for the stagnation points can be written as

Г (a) = 4n Ua sin a

which reflects the dependency of the circulation on the flap location. The pressure field is obtained from the Bernoulli equation

p(r, в) = p^ + 2p(U2 – Vr2 – V2)

On the cylinder surface this reduces to

Knowing the surface pressure distribution, one can calculate the lift and drag over the cylinder

Substituting for р(в) in the above formulae yields L’ = pUГ and D = 0, the latter being an obvious consequence of symmetry.

Another, more practical means of controlling the circulation is by giving the cylinder a rotational speed Q. Any real fluid having viscosity, the particles in contact with the cylinder will rotate at speed Q, thus entraining the nearby par­ticles through viscous shear forces to rotate also. As a result, a circulatory flow is created. The relationship between the rotation speed Q and the circulation Г is not straightforward, but can be studied numerically or experimentally. See for example the discussion, in the book by White [1], of the Magnus effect and the application to the Flettner rotor ship where the sails are replaced by rotating cylin­ders. According to Wikipedia (http://en. wikipedia. org): “Assisted by Albert Betz,

Fig. 2.10 Buckau Flettner rotor ship (from https://en. wikipedia. org/wiki/File: Buckau_Flettner_Rotor_ Ship_LOC_37764u. jpg)

Fig. 2.11 JJC demonstrating the Magnus effect

Jacob Ackeret and Ludwig Prandtl, Flettner constructed an experimental rotor ves­sel, and in October 1924 the Germaniawerft finished construction of a large two-rotor ship named Buckau. The vessel was a refitted schooner which carried two cylinders (or rotors) about 15 m (50 ft) high, and 3 m (10 ft) in diameter, driven by an electric propulsion system of 50hp (37kW) power,” Fig.2.10.

A simple experiment with a small cardboard cylinder and the flat surface of a table demonstrates the Magnus effect. A small string is wound around the cylinder and its extremity is pulled briskly to accelerate the cylinder both in translation and rotation. Depending on the sense of rotation, the cylinder will fall quickly to the ground, or fly for a short time well above the table, see Fig. 2.11.