The Ellipse at Incidence
We proceed in the same way as before. The potential, with the flow coming at an angle a from the X-axis, reads
( b2 Г
Ф = U r + cos(0 – a) – (в – a) (2.70)
r 2n
In this case, on the cylinder, the velocity components are
Г
V = 0, Ve = —2U sin (в – a) – (2.71)
2n b
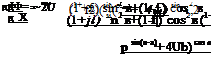 |
|
The circulation corresponding to a stagnation point at в = 0 is given by Г = 4Ub sin a. On the surface of the ellipse, after some algebra, one finds
Since the ellipse has a rounded trailing edge, there is no mechanism to control the circulation in inviscid flow and an ellipse at incidence will in general produce a flow with zero circulation. For Г = 0 the two stagnation points are located at в = a and в = ж + a, see Fig. 2.18.
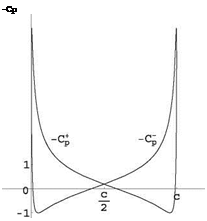
The pressure coefficient is given by
 |
||
This is represented in Fig. 2.19 as – C + and-Cp for the upper and lower surfaces, respectively.
Fig. 2.19 Pressure coefficients for the ellipse at incidence (Г — 0)
From anti-symmetry, the lift is zero. The moment however is not. It is obtained from

where O stands for the center of the ellipse, where the moment is calculated. After lengthy algebra, the result reads
The two stagnation points are now located at в — 0 and в — n + 2a. The corresponding flow is sketched in Fig. 2.20.
The surface pressure distribution for the ellipse with a small flap is shown in Fig. 2.21.
Fig. 2.20 Flow past an ellipse with a small flap at the trailing edge
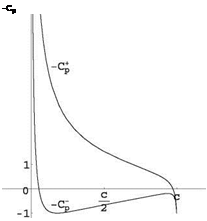 Fig. 2.21 Pressure
Fig. 2.21 Pressure
distribution on the ellipse with small flap at the trailing edge
The lift coefficient is given by the Kutta-Joukowski lift theorem
where c = 2(b2 + a2)/b. Substituting the value of the circulation gives
b2 ґ e
Ci = 4n sin a = 2n 1 + sin a (2.78)
b2 + a2 c’
The results for the cylinder and the flat plate are obtained for e/c = 1 and e/c = 0, respectively. In small perturbation theory, the term e/c can be neglected as a second – order term when multiplied by sina ~ a.











