The Flat Plate at Incidence
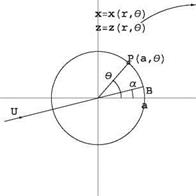
For this case, Joukowski transformation has e = 8 = 0. The flat plate is mapped into a circle with its center at the origin in the (X, Z)-plane, Fig. 2.22. The mapping can be interpreted as a conformal transformation from the cylinder plane to the physical plane such that x = Ф/U, z = Ф/U, where Ф and Ф are the velocity potential and stream function of the flow past a circular cylinder without circulation. Indeed, Eqs. (2.30) and (2.31) written in terms of X and Z read
![]()
|
 |
In this transformation, the cylinder of radius a centered at the origin, which corresponds to the stagnation streamline & = 0, is mapped onto the x-axis (z = 0), in the interval [-2a, 2a].
This case corresponds to b = a = | in Sects.2.8.1 and 2.8.2, and the results derived previously can be used.
In the mapping, the flat plate parametric representation is given by
![]()
![]() c
c
x = 2acos0 = cosQ, z = 0
2
and the velocity components in the physical plane are
дф_ (since-a)+r )
dx = 2U sin в
Forcing the circulation to be zero yields an anti-symmetric flow that does not satisfy the Kutta-Joukowski condition, Fig. 2.23. The lift is zero, but the moment coefficient about the mid-plate reduces to
Making use of the mapping, the velocity on the flat plate now reads
where the minus (plus) sign corresponds to the upper (lower) surface. The stagnation points are at x = ±2 cos a, z = 0.
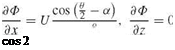 When the Kutta-Joukowski condition is applied, the velocity on the flat plate becomes
When the Kutta-Joukowski condition is applied, the velocity on the flat plate becomes
(2.85)
The streamline in this case leaves the trailing edge “smoothly”, Fig.2.24.
Note that the velocity is infinite at в = n (leading edge) in all cases except for a = 0. The stagnation point corresponds to в = n + 2a, i.e. x = -§cos2a. Itisalso worthy to note that the exact solution is consistent with the thin airfoil theory result that will be derived in the next chapter, since the flat plate is the ultimate thin airfoil, having zero thickness and zero camber. Another assumption that will be made is that of small a. If we map the flat plate to the segment [0, c] with x’ = | (1 + X) the horizontal velocity component becomes
![]() cosa ± sina — ~ U – (2.86)
cosa ± sina — ~ U – (2.86)
The plus (minus) sign corresponds to the upper (lower) surface. This last result is the thin airfoil result with a perturbation u above and below the plate that is symmetric about the x’-axis.
 Fig. 2.24 Flat plate at 25c incidence (Г = 4nasina)
Fig. 2.24 Flat plate at 25c incidence (Г = 4nasina)
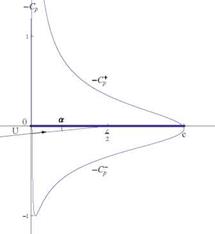
Fig. 2.25 Pressure coefficient along the plate at a = 10°
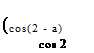 |
||
The pressure coefficient is given by
The result for-Cp is displayed in Fig. 2.25. It is not symmetric w. r.t. the Ox’-axis. If we anticipate again on thin airfoil theory, the linearized Cp will be symmetric, i. e. C – = —C+
p ^ p ■
The lift coefficient is obtained from the Kutta-Joukowski lift theorem
![]() Ci = = 2n sina
Ci = = 2n sina
2 pU 24a
It is interesting, however, to consider the integration of the pressure along the flat plate directly. The result is expected to be normal to the plate, i. e. in the z-direction. Indeed, integrating in в the elementary forces due to pressure around the plate yields the pressure contribution Fp = (0, F’p), where
F’p = 4npU2asina cosa (2.89)
On the other hand, the lift per unit span, as given by the Kutta-Joukowski theorem is
L’ = 4npU 2asina (2.90)
acting in a direction perpendicular to the incoming velocity vector as L’ = (-L’sina, L’cosa). The difference between these results is due to a horizontal suction force FS = (F’s, 0) acting at the leading edge, in the direction of the negative x-axis, that is
due to the leading edge singularity. This missing component, parallel to the camber line and of magnitude
F’s = —4npU 2asin2a (2.91)
points to the fact that integration of pressure does not capture the localized force that exists at a sharp leading edge.
The moment w. r.t. the leading edge is the sum of elementary moments
12
dM, o = —PU Cp(e)(x(в) + 2a)dx(e) (2.92)
Here, O stands for the leading edge. The moment is given by
(1 + cose)sine dв (2.93)
Some simplifications occur when the half-angle | is used. The result is
![]()
![]() 22
22
M, o = —2npU a sin2a and the moment coefficient reads
n
Cm, o = 4sin2a
For small values of a, the center of pressure for the flat plate is located at the quarter-chord.
Taking the derivative w. r.t. a of the same general formula for the moment at point D and now setting the result to zero, gives the aerodynamics center
d Cm D П X тл
— =——– cos2a +-D 2n cosa = 0 (2.97)
da 2 c
For small values of a one obtains the small perturbation result derived in the next chapter
To close this section, the limiting case of the flow coming perpendicular to the plate (a = 90°) is considered, with the plate having zero circulation or satisfying the Kutta-Joukowski condition. The two results are shown in Fig.2.26.
In Fig.2.26a, the flow is perfectly symmetric about the mid-plate and the net resulting force and moments are zero. Again, this is an idealized flow representation and viscosity will radically change the picture by having separation at the sharp edges of the plate. The same can be said of Fig. 2.26b in terms of realism of the picture, but it is intriguing to observe that there is circulation, hence lift, and the force is not perpendicular to the flat plate, but aligned with the plate and to the left. The occurrence of such a force, again a suction force, will be discussed in more details in the next chapter.