Problems
2.10.1
A 2-D model for tornadoes can be described as a core cylinder of fluid with solid body rotation and a potential vortex flow outside the core. Plot the velocity distribution and streamlines. Plot the lines of constant potentials where they exist. What is Bernoulli’s law for such a flow? Calculate the pressure distribution and in particular the pressure at the center (Hint: use normal momentum equation to calculate the pressure in the core).
2.10.2
A 2-D model for hurricanes can be described by a potential vortex and a source for the flow outside the core. Show that the streamlines are spirals. Find the velocity and pressure distributions.
2.10.3
Derive the formula for velocity distributions due to a doublet using summation of velocity vectors of a sink and a source of strength Q and a distance 2a apart, in the limit of a ^ 0 and Q ^ro, such that aQ = D.
2.10.4
Show that the velocity due to a doublet with its axis in the x-direction is the derivative with respect to x of the velocity field due to a source.
2.10.5
Show that a doublet can be produced by a pair of counter rotating potential vortices of strength Г and —Г at a distance 2a, along the z-axis, in the limit a ^ 0 and Г ^ro, such that a Г is finite (Fig.2.30).
2.10.6
Show that the velocity due to a doublet with its axis in the x-direction is the derivative w. r.t. z of the velocity field due to a potential vortex.
2.10.7
Obtain the velocity and pressure distributions around a Rankine body described by the closed streamline due to a source and a sink of equal strength and at a distance 2a apart in a uniform stream.
2.10.8
Obtain the velocity and pressure distributions around a Kelvin body described by the closed streamline due to a pair of potential vortices of equal strength and opposite direction in a uniform stream, perpendicular to their axis.
2.10.9
Show that the Joukowski transformation with e = 8 = 0, maps a circle to a flat plate with c = 4a, hence for a flat plate at incidence produces a lift C; = 2n sin a. What is the drag coefficient Cd? Explain d’Alembert paradox, considering that the pressure acting normal to the flat plate will produce a force normal to the plate and not normal to the flow direction!
|
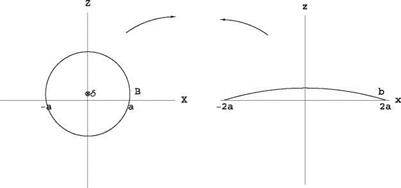
Fig. 2.30 Problem 2.10.10 |
2.10.10
Show that the Joukowskitransformation with e = 0and0 <8 ^ 1 maps a circle to a shallow circular arc as in Fig. 2.27. Find the pressure distribution over the circular arc and calculate C; and Cd. Where is the center of pressure? Where is the aerodynamic center?
2.10.11
Consider an ellipse at incidence. Show that the lift is zero. Consider next an ellipse with a small flap at the trailing edge. Find the lift (Hint: use Joukowski transformation).
Construct a symmetric airfoil with a blunt leading edge and a sharp trailing edge (Hint: use a parabola or a circle for the nose and a cubic or a quartic for the rest of the airfoil). Plot the airfoil shape.
Reference 1. White, F. M.: Fluid Mechanics, 7th edn. McGraw Hill, New York (2009)
Chapter 3