Linearization of the Pressure Coefficient

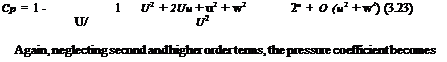This is the last element of the theory that needs to be linearized. Using Cartesian coordinates, the exact Cp can be expanded as

Cp = -2 —

p U

This expression allows for the superposition of solutions as will be needed later.

Note that the pressure coefficient only dependent on u.

Figure3.6 depicts the situation for the small perturbation analysis: a thin airfoil will disturb the uniform flow only slightly, so that, the velocity vector V in the domain surrounding the profile (with the exception of singular points) will point inside a small ball centered at the end of the undisturbed velocity vector U. The

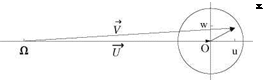direction of the velocity vector is controlled primarily by w (tangency condition), whereas the magnitude of the vector is controlled primarily by u (pressure).

Note also, that stagnation will correspond to a point located near point Q, which implies large negative values of u. In fact, the theory will allow u to go to —to at a stagnation point.