Solution of the Fundamental Integral Equation

The solution to the fundamental integral equation of thin airfoil theory has been obtained by using a change of variable that plays an important role in this theory, as well as in the Prandtl lifting line theory, as will be seen later. It is due to Glauert [1] and reads

x = §(1 – cos t), 0 < t < п (3 5

£ = §(1 – cos в), 0 < в < п (3.51)

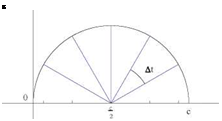
This transformation maps a uniform distribution of points on a half circle (with steps At or Ав) by projection onto its diameter (x or £). The new distribution clusters the points near the leading and trailing edges. See Fig. 3.13.

The vorticity distribution is assumed to be of the form

1 + cos в ^

Г'[£(в)] = 2U Ao + An sin пв (3.52)

I sin в n=1 J

Fig. 3.13 Geometric interpretation of the change of variable

The first term in the bracket is singular at в = 0 (leading edge) when A0 = 0. It represents the leading edge singularity. The first term by itself represents the flow past a flat plate, as will be seen shortly. Notice that this term is regular at the trailing edge as Г ‘(в) ^ 0ase ^ n. The infinite summation, the Fourier series, is the superposition of regular solutions that satisfy two K — J conditions, at the leading and trailing edges, since all the terms vanish there. In other words, the solution proposed for Г’ enforces, by construction, the K — J condition. The solution procedure consists in calculating the Fourier coefficients A0, Ai,…,An,…using the fundamental integral equation.

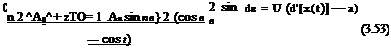Substitution of the expression for Г’ into the fundamental integral equation, and using the change of variable results in w(x, 0)

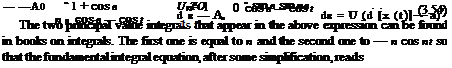or, after some rearranging

TO

d'[x(t)] — a = —A0 + An cos nt, 0 < t < n (3.55)

n=1

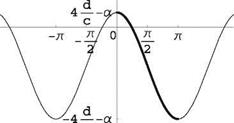
The left-hand-side is well defined for 0 < t < n. The right-hand-side is a Fourier series of period 2n. It is a series of cosines, hence even in t. Knowing its value in [0, n] is sufficient to define it for all values of its argument —to < t < to. Consider, for example, a parabolic plate at incidence a. The left-hand-side is

d x d

d [x(t)]— a = 4 1 — 2 — a = 4 cos t — a (3.56)

c V c> c

This is shown in Fig. 3.14 for d = 0.03 and a = 5° = 0.087rd.

In this particular case, the Fourier coefficients are easily found by inspection:

d

A0 = a, A1 = 4-, An = 0, n > 2 (3.57)

c

This approach can be used whenever the profile camber is a polynomial of low degree, because d'(x) can be expressed as a sum of cosines by elimination of x with t through x = 2 (1 — cos t) and use of some identities to replace cos21 by cos 2t,

Fig. 3.14 Fourier series representation for a thin parabolic cambered plate at incidence

etc.. .If the profile camber is not a polynomial, or is defined by piecewise continuous functions, the Fourier coefficients have to be calculated using the general method of integration, using orthogonality of the modes as

(3.58)

(3.59)

Note that A0 is the only coefficient which depends on a, and it is of the form

A0 = a – aadapt

where aadapt = П JC d'[x(t)]dt is a geometry related constant. When a = aadapt, the singular term vanishes (A0 = 0) and the leading edge is “adapted”, in other words satisfies the K – J condition. aadapt is called the angle of adaptation or ideal angle of attack.