Prandtl-Glauert Transformation

In subsonic flow, M0 < 1, the linearized potential flow equation is elliptic and the Prandtl-Glauert transformation reduces it to Laplace equation. Let в = – J 1 – m2 and define new dependent and

transformation and the solution to this problem is equivalent to solving for the incompressible flow past the same airfoil. For this reason, except for a finite number of singular points such as leading edge and other sharp edges, the subsonic compressible flow solution past a profile is smooth and does not admit lines of discontinuity.

Let the subscript 0 represent the incompressible solution, i. e. at Mach M0 = 0. The pressure coefficient is modified as follows

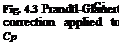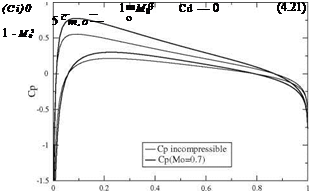where (Cp)0 = -2j, see Fig.4.3. The forces and moments at Mach number M0 will also be divided by 1 – M2, which is the Prandtl-Glauert rule

Note that the drag is still zero. To be complete, one can add that the center of pressure and the aerodynamic center coincide with their incompressible counterparts.