2D Boundary Layer Solution Methods – Overview

4.10.1 Classical boundary layer problem

The classical incompressible 2D wall boundary layer problem has the following inputs and outputs.

Inputs: Outputs:

v or Reref viscosity or Reynolds number u(s, n),v(s, n) velocity field

ue(s) edge velocity distribution 5*(s),6(s) … thicknesses, from u(s, n)

u0(n),v0(n) initial velocities at s0 H(s),Cf (s) shape parameter, skin friction

The inputs are quantities which appear in the boundary layer equations (4.21) and boundary conditions (4.22). The outputs are the unknowns in these equations, or functions of these unknowns.

The initial velocities u0,v0 at the first location s0 (shown in Figure 4.22) are not needed if this is a leading edge or stagnation point, which is the most common situation. In this case they can be taken from one of the self-similar solutions treated earlier.

4.10.2 Finite-difference solution methods

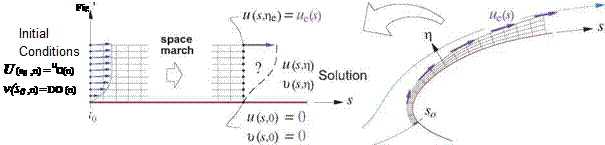The most general solution approach is the grid-based finite-difference method, sketched in Figure 4.22. The solution procedure solves for all the u, v unknowns at one s station at a time, starting at the first s0 station. This solution procedure is known as space marching. For details, see Cebeci and Smith [19], Cebeci and Bradshaw [20].

For the general boundary layer problem, the space-marching finite-difference solution procedure is accurate and effective, but requires considerable computational effort. For acceptable accuracy for laminar flows, it requires at least 20 or more grid nodes across the layer at each surface point, with the three u, v, т unknowns per grid node. Turbulent flows may require 80 or more grid nodes per surface point. A typical ue(s) dis­tribution, over an airfoil surface say, might require over 100 surface points, resulting in many thousands of unknowns for the entire 2D boundary layer. When the boundary layer is to be solved simultaneously with the potential flow, as will be described in Section 4.12.2, this large total number of unknowns is prohibitive. Another drawback of the finite-difference method is that it is purely numerical, and gives no direct insight into boundary layer behavior. An alternative approach is taken by the integral methods, described next.