Cambered body of revolution

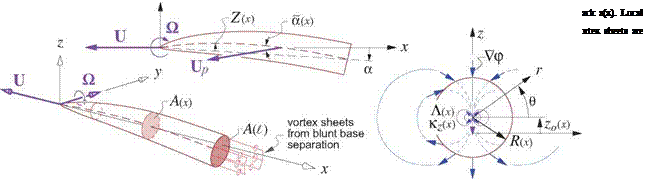
A cambered body with circular cross sections is shown in Figure 6.11. Its surface geometry is defined by

r(x, e) = x x + [ R cos 9 ] y + [ R sin 9 + Z — ax ] z (6.70)

where Z(x) is the camber of the centerline, a is the overall body angle of attack, and R(x) is the radius of the local circular cross-section which is centered on z = z0(x) = Z(x) — ax.

The local normal vector is computed from (6.70) using the cross-product relation (6.61), with 9 = s/R.

(6.71)

z

In terms of the cross-sectional area A(x) = nR2, the far-field source and doublet strengths are

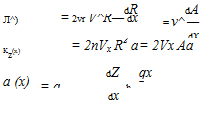(6.72)

(6.73)

(6.71) where a is the local angle of attack of the body centerline relative to the local body velocity U/(. The potential expression (6.66) with the strengths (6.72),(6.73), and the geometry given by (6.70) all together
exactly satisfy the 2D Laplace’s equation (6.62) and boundary conditions (6.63), (6.64). Therefore this far-field flow happens to be an exact solution of the transverse-flow equations for this geometry.

With the z-doublet strength known, the overall lift can be obtained by integration of the lift gradient (6.69).

L = j ^ da: = pV2 ёж = PVJ£ Add «№ (6.75)

This final result shows that within the assumptions of potential flow, the lift of a slender body of revolution depends only on its base area A(e) and the local angle of attack d(£) at the base location. Trefftz-plane analysis requires that any lifting body must generate trailing vorticity, and indeed the blunt base will shed the necessary vortex sheets as sketched in Figure 6.11. A related conclusion is that bodies which come to a sharp point at the rear cannot generate lift, since they cannot shed vorticity in the absence of flow separation.

The lift distribution dL/dx will also produce the following overall pitching moment (positive about the y axis) about the x = 0 reference point.

Mo = f —x-r~ ёж = pV2 f—x dx = — pV2 £ Ap) d{£) + pV2 f Ad ёж (6.76)

Jo dx о dx о

With zero base area and zero camber the lift is zero, and the pitching moment simplifies to

r f­M = pV2 a A dx = pV2 V a (6.77)

о

about any reference point x location, where V = /0A dx is the body’s volume. An important result is dM/da = pV2 V > 0. An angle of attack change да will therefore produce a pitching moment change AM of the same sign, which will tend to increase да even more. A body of revolution therefore exhibits an inherent pitch instability, which must be stabilized using fins as on a blimp or submarine, or gyroscopically via axial spin as on a finless projectile or a football thrown with a “spiral.”

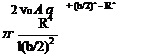The results above have also been obtained by Ashley and Landahl [50] who used complex mapping to define the transverse flow. They also assumed a more general “finned” body of revolution with local span b(x) whose cross-section is shown in Figure 6.12. The local z-doublet for this case can be given in terms of an effective area A1,

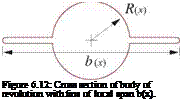while the local lift relation (6.69) remains the same. The total lift and moment is therefore given by ex­pressions (6.75) and (6.76) if the area A is replaced by the effective area A1 defined above. For the case b/2 = R where the fins have zero width, we have A1 = A, and the finned-body results reduce to the circular cross-section body results as expected.