Subsonic Compressible Far-Fields
8.7.1 Far-field definition approaches
Two approaches can be used to define the far-field for any given compressible flow situation:
1. Define the far-field expansion in physical space. A complication now is that the integrals for the far – field coefficients must include contributions from the field sources. For example, the 2D far-field x-doublet strength of an airfoil represented by source and vortex sheets is
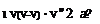
![]() kx = j (—Xx’ + yz’) ds’ +
kx = j (—Xx’ + yz’) ds’ +
where the last integral over the field sources x(x’,z’) would be difficult or impractical to compute in practice.
2. Define the far-field expansion in Prandtl-Glauert space. Now the x-doublet strength is
![]() Kx = (-Xx’ + yz’) ds’
Kx = (-Xx’ + yz’) ds’
in which the field source integral does not appear, since X ~ 0 within the transformed flow-field. Existing incompressible-flow estimates for the coefficients can therefore be used. The resulting transformed far – field potential or velocities are then reverse-transformed to obtain the physical potential or velocities. This far-field definition approach is clearly better, and will be used here.











