Adjoint-Based Error Estimation and Functional Correction

An efficient and consistent way of estimating numerical errors in a functional I(U) of interest, are the so-called dual weighted residual approaches (DWR). Here, one weights the numerical error, represented by the residual R(Uh) of the numerical state solution Uh approximating the exact solution U, by the so-called dual or ad­joint state. The idea stems from Johnson, Rannacher et al. [6] in the Finite Element Method (FEM) context. The reason for the weighting of the (local) residual with the adjoint field vector у is, because the adjoint is an influence function (i. e. a Green’s function) w. r.t. the functional of interest I, for which one has solved the adjoint state equation

The adjoint field vector has value zero in areas with no impact on the functional I(U), and (very) different from zero in areas of (big) impact. This means, that the adjoint as a weight eliminates local residuals in areas where the error only appears, and increases it in areas where the errors come from.

Unfortunately, there is a difficulty in transfering the DWR to Finite Volume Methods (FVM). The reason is, that one would need the exact adjoint solution for the calculation of the first order error term. Instead, one solves in FEM context the adjoint problem with higher order test and ansatz functions, and this yields then the first order error estimate. But in standard FVM, it is not possible to play around with the order of test and ansatz functions.

One possibility to overcome this difficulty is the repeated extrapolation between certain mesh levels (e. g. from coarse level H to globally refined level h) as suggested by Venditty and Darmofal [13] or Pierce and Giles [10]. This approach has been proved to lead to a good error estimate, given as

Ih(UH) – Ih(Uh)« {whHГRh(UH), (11)

but is not handy e. g. in areas of shocks and w. r.t. memory consumption (due to values needed at globally refined mesh level h).

An alternative idea by Dwight [5] is, to interpret the discretization error R(Uh), at least for the central Jameson-Schmidt-Turkel scheme available in TAU, as dissip­ation error. This yields instead of

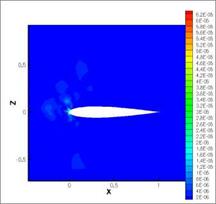
Fig. 15 Adjoint-based error sensor for lift (left) and drag (right) to the error estimate

m,)-m « vf (t,2) H+t’41^i) • (13>

Here, k(2) and k(4) are the scaling coefficients for the dissipation of second and forth differences, i. e. first and third order. It turns out that this approach is accurate enough and obviously it is very handy.

This method has been implemented by R. Dwight in the TAU code and has been used by the authors within the project MUNA.

The right hand side of Equation (13), the global error estimate, is to be under­stood as the integral or sum of the local error estimates

at cell positions Xi, j,k, and (14) can be used as an indicator or sensor for adjoint – based (and therefore) goal-oriented mesh adaptation. For the realization and applic­ation of this local adjoint-based sensor for mesh adaptation in TAU, we refer to Section 5.

In this Section we first present the validation of the local and global adjoint-based error estimate. The difficulty in the validation here is, that one should know about the exact solution to compare with. Therefore, we have chosen an inviscid subsonic NACA0012 flow case and drag as functional of interest. Then we know, that the exact (shock less) solution has zero drag. (Only some spurious drag, i. e. numerical dissipation, remains.)

Figure 15 shows the local sensor (14) for lift and drag. That these sensors, which are the local error estimates, lead to good global error estimates, can be seen in Figure 16.

Furthermore, the adjoint method is used for the efficient quantification of uncer­tainties in the aerodynamic coefficients caused by variations of the model

Adjoint Based Error Estimate / Functional Correction

NACA0012

Ma = 0.5 a = 1.0°

Q

О

Adaptation

Fig. 16 Adjoint-based global error estimation and functional correction for the drag coeffi­cient on initial and globally refined mesh (NACA0012, Ma = 0.5, a = 1.0°, inviscid) parameters of the SAE and the Wilcox-k-ю turbulence model. Compared to finite differences one is here independent of the number of model parameters w. r.t. the nu­merical costs. Figures 17 and 18 show a good match of the sensitivities calculated by the adjoint method as well as by finite differences for lift and drag coefficients, caused by variations in the model parameters of SAE and Wilcox-k-ю.