SINUSOIDAL INPUT—NYQUIST CRITERION

The above consideration of pulse trains (which can be so easily analyzed) has shown the important effects of loop gain and phase lag on system stability.

These concepts are brought into a somewhat more useful perspective when we consider a sinusoidal input, for all inputs to linear systems can be Fourier – analyzed into separate sinusoids, the individual responses to which can be linearly superposed to construct the output. Suppose then that there is a steady sinusoidal input represented by

x = X0eiat

and a steady sinusoidal output

У = Y0ei<at

(This implies of course that the system is stable.) The error is e = x — у = e0eim*, where e0 = X0 — Y0. Now we recognize that the critical phase lag is 180°, since this generates the maximum error signal, just as in the case of the pulse train. So let

Y0 = Ке0е-™ = – K4

Then we get

= ea + Гв — r0 — YJK

The input required to maintain a steady oscillation of given amplitude is seen to diminish as К increases until it vanishes altogether at К = 1, i. e.

at К — 1 and phase lag of 180°, the system oscillates steadily with no input. This situation clearly represents a stability boundary; further increase in gain corresponds to instability.

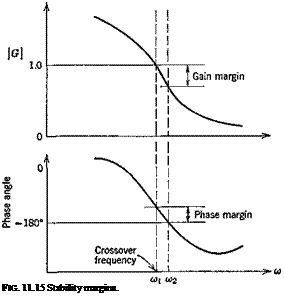
The Nyquist criterion (11.4) rigorously derived from a theorem of Cauchy contains the conclusion derived somewhat heuristically above. It uses the frequency response curve for the open-loop system, i. e. G(ioo), and its relation to the point (—1, 0) of the complex plane, to assess stability. The amount by which the frequency response curve “misses” the critical point (—1, 0) leads to the concepts “gain margin” and “phase margin” illustrated in Fig. 11.15.