Control Force Gradient

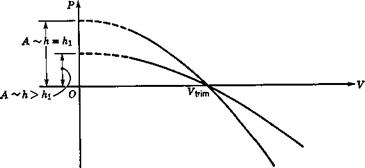
It was pointed out in Sec. 2.7 how the trim tabs can be used to reduce the control force to zero. A significant handling characteristic is the gradient of P with V at P = 0. The manner in which this changes as the CG is moved aft is illustrated in Fig. 2.28. The trim tab is assumed to be set so as to keep Vtrim the same. The gradient dP/dV is seen to decrease in magnitude as the CG moves backward. When it is at the control-free neutral point, A = 0 for aircraft with or without tails, and, under the stated conditions, the P/V graph becomes a straight line lying on the V axis. This is an important characteristic of the control-free NP; that is, when the CG is at that point, no force is required to change the trim speed.

A quantitative analysis of the control-force gradient follows.

The force is given by (2.8,9). From it we obtain the derivative

dP

w-w

At the speed Vtrim, P = 0, and В = —A/|pV2trim, whence

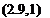
Э P _ 2A

av “ _

A is given following (2.8,9). Substituting the value into (2.9,1) we get

dP a’b2 w

— = 2GSece — — (ft – K) dV det Vlrim

From (2.9,2) we deduce the following:

1. The control-force gradient is proportional to Sece; that is, to the cube of air­plane size.

2. It is inversely proportional to the trim speed; i. e. it increases with decreasing speed. This effect is also evident in Fig. 2.27.

3. It is directly proportional to wing loading.

4. It is independent of height for a given true airspeed, but decreases with height for a fixed VE.

5. It is directly proportional to the control-free static margin.

Thus, in the absence of Mach number effects, the elevator control will be “heaviest” at sea-level, low-speed, forward CG, and maximum weight.