THE NONLINEAR MODEL

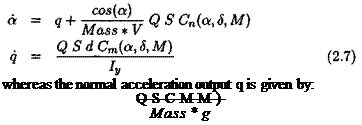A nonlinear longitudinal missile model is extracted from (Reichert, 1992). The control input is the tail deflection <5, while the outputs used by the autopilot are the acceleration and rate outputs [ту, q). The state vector is [ct, <?], where a is the angle of attack. The missile behavior can be described by the following nonlinear equations:

This model is essentially parameterized by the Mach number M (between 2 and 4). The dynamic pressure 0, the reference area S, the diameter d, the pitch moment of inertia Iy and the missile mass are indeed constant, while the missile velocity V is proportional to M. Cn and Cm depend on M, a and 8:

Cn(a,8,M) = ana3 + bnaa + c„(2 – M/3)a + dn8 Cm(a,8,M) = ama3 + bmaa + cTO(—7 + 8M/3)a + dmS (2.9)

See (Reichert, 1992) for numerical data. The main nonlinearities are the variation of Cn(a,8,M) and Cm(a, S,M) as a function of a, since these quantities are third order polynomials of a, whose range of variation is ± 20degrees. The actuator is finally a second order transfer function:

Hact{s) = – Г2 ~~2fZTT~T (2.10)

with u>act = 1 5 0 rad/s and £act = 0.7.