Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
A SECOND ц BASED METHOD
The sufficient condition of non oscillation is introduced in the first subsection. The method is extended to the case of parametric uncertainties in the second subsection. The third subsection shows that a skewed H problem with a special structure is to be solved. The problem of using (skewed) /г bounds is discussed in the last subsection.
3.2 A SUFFICIENT CONDITION OF NON OSCILLATION
|
|
monic part e(£) of the signal u(t), at the output of the nonlinearity Ф. To this aim, the frequency response of the nonlinearity is rewritten as N(X, uj) + Д, where Д represents the error induced by the SIDF approximation.
• In the case of a SISO nonlinearity, Д is known by the relation:
|
|
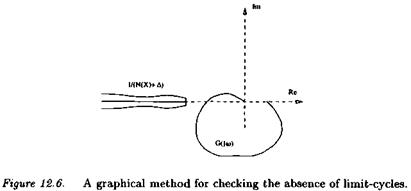
where a( X, a( is a function of X and ш. With respect to Figure 12.1, a sufficient condition of non oscillation is then that the inverse of the frequency response X( X, a) X Д of the nonlinear element does not intersect the frequency response of the linear part G(s) of the closed loop. As in section 2.1, when N(X, w) and a{X, u>) do not depend on frequency u>, Figure 12.6 suggests a graphical method for checking the absence of limit-cycles.
|
|
• In the case of a MIMO nonlinearity, Д is known by the relation:
a(A)<a(X, u) (12.32)
|
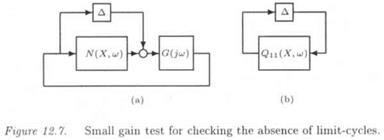
Figure 12.1 is transformed into Figure 12.7. a, by replacing the nonlinearity Ф by its frequency response N(X, u>) + A. Figure 12.7.a is then transformed into Figure 12.7.b, where Qn(X, w) is the transfer seen by Д in Figure 12.7.a Applying finally the small gain theorem to Figure 12.7.b, a sufficient condition of non oscillation is obtained as:
|
where Д satisfies equation (12.32). The sufficient condition of non oscillation thus becomes:
|
|
