Application of the Similarity Method

The word similarity is used in several contexts throughout this book. There is a sig­nificant probability that the student is becoming confused from the frequent appear­ance of this terminology in seemingly different uses of the same word. Therefore, the several meanings are reviewed briefly, as follows:

1. Geometric Similarity. This describes two or more body shapes that are exact photographic images (i. e., enlargement or reduction) of one another.

2. Similarity Parameters. These are dimensionless quantities that can be deduced from dimensional-analysis considerations or from experiment—for example, the Mach number, Re number, and lift coefficient. These are especially useful in presenting results or when planning experiments.

3. Similarity Relationships. These are functional relationships between similarity parameters. They may be explicit when equation solutions may be found, or functional in form if the defining equation is difficult to solve, as in nonlinear – flow problems.

4. Dynamic Similarity. If two geometrically similar bodies are in two flows that have the same values of the pertinent similarity parameters, then the two flows are dynamically similar. The pertinent similarity parameters may be found by dimensional analysis or by writing the defining equations for that class of problem in nondimensional form. Similarity parameters appear as coefficients in the equations. For example, if the laminar boundary-layer equations for incompressible flow are written in nondimensional form, the only parameter that appears is the Re number. Hence, a known solution to the equations for one flow problem also is a solution (in nondimensional form) to a second flow problem, provided that the two flows have the same Re number. For com­pressible flow, additional pertinent similarity parameters usually are the Mach number, Prandtl number, and ratio of specific heats, y. Dynamically similar flows have equal-force coefficients.

5. Similarity Rules. Two flow problems can be called similar in the sense that they are related by a coordinate transformation connecting the two defining equations and the two sets of appropriate boundary conditions. Certain scale factors arise that relate to the pressure and force coefficients and the shape of the two bodies in the two flows.

6. Similarity Solutions. These are methods of solution in which mathematical advantage may be taken if the solution at one station in a flow is geometri­cally similar to solutions at other stations. For example, in certain boundary layers, the velocity profiles are of the same mathematical family. When this hap­pens, it becomes possible to construct a new independent variable—which is a
combination of the original dependent variables—such that the derivatives in the governing equation(s) all can be written as derivatives of this new indepen­dent variable. For two-dimensional, viscous-flow problems, partial-differential equations become ordinary differential equations when similar solutions are assumed. Similar solutions in viscous flow involve “self-similar” velocity profiles, meaning that the profiles collapse to a single curve when graphed in appropriate coordinates. An example is the velocity profile in the incompressible boundary layer growing along a flat plate.

7. Similitude. Two flow problems have similitude if they have identical defining equations and boundary conditions when written in dimensionless form.

It is in the context of the sixth meaning that we are working herein. Referring to Fig. 8.10, notice that we expect the flat-plate boundary layer to increase in thick­ness as the distance from the leading edge is increased. It is certainly plausible that the velocity distribution across this thickness would be “similar” at any station. We now examine the differential equations to see if this is a possible outcome, which is accomplished by checking whether the equation and the boundary conditions are unaffected by an affine transformation. Such a transformation is one in which a parameter—say, X—or its powers can be used to scale each variable without changing the form of the mathematical problem. That is, the problem is invariant to the transformation.

If the differential equation for the stream function (Eq. 8.40) and the four boundary conditions (Eq. 8.41) are transformed in this manner by setting:

y = Xy’

л n f

• x = X x (8.41)

z = Xm z’

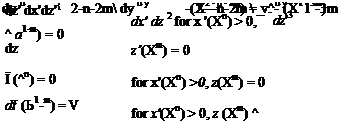where the primes denote the “stretched” variables, we find that the problem is now governed by:

^(X1-m) = У for x'(Xn) = 0, z(Xm) > 0

I. dz ”

For a similarity solution to be available, it is necessary for all occurrences of the parameter X to disappear in the transformed equations. This is so only if:

X2-n-2m _ X^3m

and X1-m = 1.

Notice that the boundary conditions requiring zero values are unaffected by the transformation. Therefore, for a similarity solution, it is necessary only that m = 1 and n = 2. Then, Eq. 8.43 reduces to the same set before the transformation. The real benefit from the transformation process begun here is that it suggests that we can combine the original independent variables such that the number of variables required in the problem can be reduced. For instance, the combination:

yields such a result. Notice that the new combined “length” variable does not have the dimensions of length but rather the square root of length. It is often better to work with dimensionless variables, so we seek to introduce appropriate scaling factors from the natural parameters in the problem to render the transformed problem in dimensionless form. The velocity of the uniform parallel flow outside the boundary layer, Ue = Vж can used as a reference velocity. Since there is no natural length scale of the sort present in the Couette and Poiseuille flows, it is necessry to use the parameters in the differential equation to form an equivalent reference length. Notice that the combination:

v [ft2/sec]

Ue ^ [ft/sec]

has the dimensions of length, so all the dimensional length variables like x and y or X and y can be rendered dimensionless by dividing by v/Ue. Therefore, if we replace x and y and X and y’ by their dimensionless equivalents in Eq. (8.45) we can define a dimensionless transformed coordinate, n as:

Combining the original dependent variable, y, with the original independent vari­ables can result in a new dependent variable that is independent of the parameter X. Call the new (dimensionless) dependent variable f, which we assume will be a function only of the new single dependent variable n. To eliminate the X in the transformed stream function, we note that x = XV so х = 4ХЇХ and f can then be defined in dimensionless form as:

which satisfies the criterion that parameter X does not appear explicitly. The param­eters within the square brackets represent the dimensions of the stream function and the inverse square root of the characteristic length. Since f is dimensionless by definition, we can then write the (dimensional) stream function as:

y(*. ^ = 4vU*x ^(n)

The detailed steps we have shown here are not usually presented in undergraduate textbooks. What is often done is to introduce the results shown in Eqs. (8.46) and (8.47) as assumptions with little justification other than that “it works.” Although you may have trouble understanding fully the significance of the similarity trans­formation process in a single reading, you are invited to study the steps again when confronted in the future by problems that may require a similiarity solution.

Now, to see if this new set of variables represents any kind of an advantage, we attempt to rewrite Eqs. 8.40 and 8.41 in terms of n and f. Several derivatives must be evaluated, so we note first that:

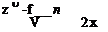= ZK±X~ 2

dx V V dx

dn= —

dz V VX

Please keep in mind as we use these results that we are transforming the set of independent variables (x, z) to the new set of independent variables (x, n). Care must be taken in the differentiation process. The derivatives of any function with respect to the original variables must now be written as:

d^d+dpd_d n d

dx dx cX dp cX 2 x dp

2^элА_ U_d_

dz dz dp V VX dp

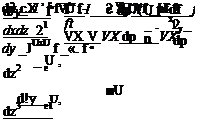so that the derivatives needed in Eq. (8.40) are:

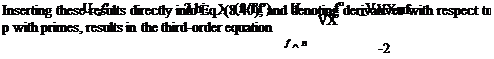
The Blasius Flat Plate Boundary-Layer Equation

and after simplifying,

2 f"’ + ff "= 0 (8.49)

which is often called the Blasius boundary layer equation. The boundary conditions in like fashion simplify to

[ f ‘(0) = 0

{f (0) = 0 (8.50)

1 f'(~) = 1

since f is a function of n only. The original complex partial differential equation reduces to a simple (but nonlinear!) ordinary equation. Since Eq. 8.50 is nonlinear it is necessary to apply numerical methods for its solution. Another feature requiring special attention is that the boundary conditions must be satisfied at two widely separated locations (n = 0, and n = 0). This means that we must solve a two-point boundary value problem by numerical means. Many approaches have been devel­oped in the years since Blasius presented his Ph. D. thesis work. Many of these were developed before the ready availability of fast digital computers, so they necessarily employed a variety of mathematical strategems that are no longer needed and are therefore not discussed here. The problem can now readily be handled on your per­sonal computer or even a good programmable hand calculator.

For example, one can easily solve the problem using a simple fourth-order Runge-Kutta integrator and a simple shooting method to deal with the two-point boundary value features. Equation (8.50) is first broken down into three simul­taneous first-order ordinary differential equations. For example, one can write

where the first two equations simply define the derivatives of the variable f. Since there is no boundary condition on h, (equivalent to the second derivative of f with respect to n, then we can adjust this value until g = 1 at a large value of the indepen­dent variable n. Newton’s method or a similar technique can be used to adjust an initial guess for h at n = 0. It is not necessary to carry the integration to a large value of n. Experience shows that once a value of about 10 is reached, this is effectively infinite on the scale of n. The detailed calculation is left to the student in a problem at the end of this chapter.

Numerical results from this procedure are shown in Table 8.1 and Fig. 8.11a. Notice that in Fig. 8.11a, the plot for f versus h is a representation for the velocity distribution through the boundary layer if f is proportional to the x-velocity, as indi­cated in Eq. 8.47. That is, the x-velocity component through the layers is:

n	f	f ‘	f"
0.0	0.00000	0.00000	0.33206
0.5	0.04149	0.16589	0.33091
1.0	0.16557	0.32978	0.32301
1.5	0.37014	0.48679	0.30258
2.0	0.65003	0.62977	0.26675
2.5	0.99631	0.75126	0.21741
3.0	1.39681	0.84605	0.16136
3.5	1.83770	0.91304	0.10777
4.0	2.30575	0.95552	0.06423
4.5	2.79014	0.97952	0.03398
5.0	3.28328	0.99154	0.01591
5.5	3.78058	0.99688	0.00658
6.0	4.27963	0.99897	0.00240
6.5	4.77933	0.99970	0.00077
7.0	5.27925	0.99992	0.00022
7.5	5.77923	0.99998	0.00006
8.0	6.27922	1.00000	0.00001
8.5	6.77922	1.00000	0.00000
9.0	7.27922	1.00000	0.00000
9.5	7.77922	1.00000	0.00000
10.0	8.27922	1.00000	0.00000

Table 8.1. Function f and its derivatives

where Eq. 8.48 for the z-derivative is used. Thus, the solid curve in Fig. 8.11 is the famous Blasius laminar-velocity profile for a flat-plate boundary layer. Carefully measured velocity profiles show essentially exact agreement with the theoretical predictions from the Blasius analysis shown in Fig. 8.11a.