Potential Flow
2.1.1 Equation of Motion
Let us write the velocity vector q in Cartesian coordinates as q = ui + v j + wk. Here, и, v and w denotes the velocity components in x, y, z directions, and i, j, k shows the corresponding unit vectors. At this stage it is useful to define the following vector operators.
U. Gulfat, Fundamentals of Modern Unsteady Aerodynamics, 23
DOI: 10.1007/978-3-642-14761-6_2, © Springer-Verlag Berlin Heidelberg 2010
The divergence of the velocity vector is given by
Ou Ov Ow div q = V. q = + +
Ox Oy Oz
and the curl
i j k
![]() AAA
AAA
Ox Oy O z
u v w
The gradient of any function, on the other hand, reads as
Of Of Of
gradf=Vf=f+ff
The material or the total derivative as an operator is shown with
D 0 0 0 0
= +u +v +w Dt Ot Ox Oy Oz
Here, t denotes the time. Now, we can give the equations associated with the laws of classical mechanics.
|
Dq Equation of continuity: + qV. q = 0 |
(2.1) |
|
Dq 1 Momentum equation: H—V p = 0 |
(2.2) |
|
D f a2 q2 1 Op E“rgyequa, i°n: Dt у – 1 + 2 = q Ot |
(2.3) |
|
Equation of state: p = qRT |
(2.4) |
Here, the pressure is denoted with p, density with q, temperature with T, speed of sound with a, specific heat ratio with у and the gas constant with R.
In addition, the air is assumed to be a perfect gas and the body and frictional forces are neglected. It is also assumed that no chemical reaction takes place during the motion. The energy equation is given in BAH.
Let us now see the useful results of Kelvin’s theorem under the assumptions made above (Batchelor 1979). The following line integral on a closed path defines the
Circulation: Г = q • ds.
![]() The Kelvin’s theorem:
The Kelvin’s theorem:
Dt
For incompressible flow or a barotropic flow where p = p(p) the right hand side of Kelvin’s theorem vanishes to yield
![]() ОГ
ОГ
~Dt
This tells us that the circulation under these conditions remains the same with time. Now, let us analyze the flow with constant free stream which is the most referred flow case in aerodynamics. Since the free stream is constant then its circulation Г = 0. The Stokes theorem states that
q • ds = x q • dA = 0 (2.5)
The integrand of the double integral must be zero in order to have Eq. 2.5 equal to zero for arbitrary differential area element. This gives V x q = 0.
V x q = 0, on the other hand, implies that the velocity vector q can be obtained from the gradient of a scalar potential /, i. e.
q = V / (2.6)
At this stage if we expand the first term of the momentum equation into its local and convective derivative terms, and express the convective terms with its vector equivalent we obtain
Oq 1 q2
+ (q • V)q = —Vp and (q – V)q = V – – q x (V x q). ot p 2
From Eq. 2.5 we obtained V x q = 0. Utilizing this fact the momentum equation reads as
![]() oq q2 1
oq q2 1
+ V – +—Vp = 0 ot 2 p
Now, we can use the scalar potential / in the momentum equation in terms of Eq. 2.6.
For a baratropic flow we have the 3rd term of Eq. 2.7 as
1 dp
-Vp = V
pp
Then collecting all the terms of Eq. 2.7 together
V-10/ – £-/ dp) = 0
we see that the scalar term under gradient operator is in general only depends on time, i. e.,
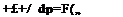
![]() 0/ q2 dp
0/ q2 dp
07 + "2"
According to Eq. 2.8, F(t) is arbitrarily chosen, and if we set it to be zero we obtain the classical Kelvin’s equation
![]() 0/+7+/dP=»
0/+7+/dP=»
Let us try to write the continuity equation, Eq. 2.1, in terms of / only,
![]() 0q / ,
0q / ,
-07 + (q – v) p + pv-q = о
The gradient of the velocity vector now reads as
V-q = V2/.
 |
Dividing Eq. 2.10 by p we obtain
Now, let us write Eq. 2.7 in terms of / and the pressure gradient. Furthermore, expressing the pressure gradient in terms of the density gradient and the local speed of sound we obtain
![]()
![]() 1 a2
1 a2
-Vp = Vp
p p
and with the aid of Eq. 2.14 and the multiplying term q/a2, the final form of Eq. 2.11 reads as
In Eq. 2.15, we express the velocity vector in terms of the velocity potential. This way, the scalar non linear equation has the scalar function as the only unknown except the speed of sound. The equation itself models many kinds of aerodynamic problems. We need to impose, however, the boundary conditions in order to model a specific problem.











