Unsteady Flow
Our unsteady analysis of the flow is going to be similar to that of steady flow except now, we are going to assume a vortex sheet strength ya = ya (x, t) as the function of two variables x and t. There will also be continuous vortex shedding to the wake from the trailing edge because of having unequal vortex sheet strength from the lower and upper surfaces right at the trailing edge. Since there is a vortex sheet at the near wake there will be a velocity field induced by it as well as its effect on the bound vorticity. Let us now see the effect of the both vortex sheets on the induced downwash with the aid of Fig. 3.6.
Denoting the near wake vortex sheet strength with yw, the downwash w at z = 0 with the aid of Biot-Savart law
b 1
![]()
![]() 1 f Уа(П; t)dn _ 1 f Cwfe t)dn
1 f Уа(П; t)dn _ 1 f Cwfe t)dn
2p x _ П 2p x _ П
_b b
The first integral at the right hand side of Eq. 3.9 is singular but the second integral is not. We can write the equivalent of the second integral in terms of the bound vortex using the unsteady Kutta condition.
In case of steady flow we have expressed the Kutta condition as the zero velocity at the trailing edge or no vortex sheet at the near wake or no pressure difference at the wake region. In case of unsteady flow, however, there is a nonzero velocity at the trailing edge and non zero vortex sheet at the near wake. Therefore, the unsteady Kutta condition is expressed as the zero pressure difference at the wake. Accordingly, the unsteady Kutta condition is more restrictive, and therefore in formulation it reads
In terms of perturbation potential, using Eq. 2.21 it becomes
Equation 3.1 gives the relation between the perturbation potential and the vortex sheet strength for the steady flow case. Similarly, we can write this relation for the unsteady flows at any time t as follows
The integral relation between the perturbation potential and the perturbation velocities are
X X X X
/U = J 0/rdn = j UUdn ve /i = J 0/dn = j uidn
—1 —1 —1 —1
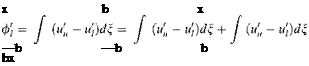 |
|
Before the leading edge we do not have any velocity discontinuity between upper and lower surfaces therefore, for x < —b there is not any contribution to the integrals evaluated for x > b
If we take the derivatives of the above expression with respect to t and x, the unsteady Kutta condition becomes
The first integral at the left hand side is evaluated to the bound vortex Га (t). Hence, the final form of the unsteady Kutta condition reads
X
~ГГ + 0J t’)dn + U ^ ^=0 (3’10)
b
Equation 3.10 is an integro-differential equation which relates the bound vortex to the vortex sheet strength of the wake. Our aim here is to eliminate the wake vorticity appearance from the downwash expression so that all the terms in Eq. 3.9 are expressed in terms of the bound vortex sheet strength. If we transform time coordinate to some other coordinate and then differentiate the result with respect to x we can succeed to do so. Let us now take the Laplace transform of Eq. 3.10, remembering the definition and a property of the Laplace transform (Hildebrand
1976) ,
Lff(t)g e slf(t)dt = я» and L{~dr}= sf(s)~/(0+)’
0
The Laplace transform of 3.10 then becomes
X
sCa + J syw(n, s)dn + UCw(x, s)= 0 (3:11)
b
Here, at t = 0+, Га and yw (x) are both zero. If we take the derivative of Eq. 3.11 with respect to x, the first term becomes zero and we end up with a first order differential equation in x.
sCw(-T s) + U0xCw(x; s)= 0 (3’12)
The solution to this equation becomes
Cw(-T s) = B(s)e U’
In order to determine B(s) we utilize the value of 3.10 at x = b. This gives
sC
sfa + Uyw(b, s) = 0 and yw(b, s) = B(s)e—U combined B(s) = — aeU:
substituting B(s) gives
![]() sCae U(x b) or with x* = x/b U ‘
sCae U(x b) or with x* = x/b U ‘
![]()
|
|
|||
|
|
|||
![]()
|
|
|
|
|
|
|
|
|
|
|
|
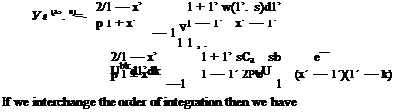 |
|
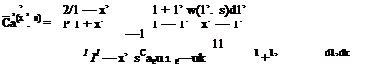 |
|
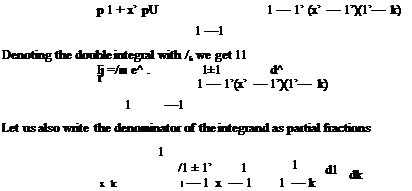 |
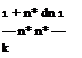 |
|||
and evaluate the inner integrals as follows
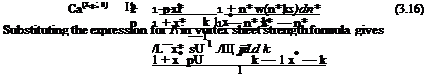 |
Adding those two together
In Eq. 3.16, the bound vortex Га plays the role of a coefficient at the right hand side to determine the bound vortex sheet strength itself. Therefore, if we integrate 3.16 with respect to full chord we obtain the bound vortex also. In non dimensional coordinates the integral reads as
If we interchange the order of integrals at the right hand side, we can then perform the integrations with respect to x* and obtain the following equation Га in terms of the downwash
The second term at the right hand side of Eq. 3.17 can be integrated with respect to k. The resulting integral is expressible as an Hankel function of second
kind in terms of the complex argument (-isb/U). A useful relation between the Bessel functions and the Hankel functions are provided in Appendix 5.
Denoting the integral at the second term of Eq. 3.17 by I2 with the help from Theodorsen, we obtain
1
and write the result for the bound circulation in terms of the downwash
![]()
![]()
![]()
![]()
![]() (3.19)
(3.19)
The relation between the downwash w and the time dependent motion of the airfoil was given by Eq. 2.20. We need the Laplace transformed form of Eq. 2.20 to implement in 3.19, which is
w(X*, s) = sZa(X*; s)+ +bO0^Za(X*, s)] (3.20>
At this stage, we can use 3.20 in 3.19 and obtain the bound circulation in s domain. After inverting the result to time domain by inverse Laplace transform, we can get the time dependent bound circulation and the lift. For more detailed analysis, the relation between the lifting pressure coefficients and the bound vortex sheet strength we obtain
x
. . 2 0 2 0/ 0/ 2 0 2 cPa(x,,) = UT* 05(/-/’) + U?(aT – = U 0,J ‘!-(i-,)dn + v>a(x, t)
-b
(3.21)
We can now take the Laplace transform of Eq. 3.21 which in s domain reads as
Substituting Eq. 3.16 in 3.20 and integrating the fist term on the right hand side we obtain
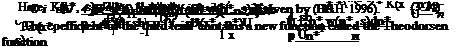
(3.23)
Functions F and G are real although their arguments are imaginary. The The – odorsen function takes the value of unity for s approaching to zero, i. e.
![]() й C ‘U
й C ‘U
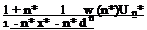
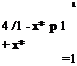 |
which simplifies the pressure coefficient for s = 0 as follows
This term is called the quasi steady pressure term and it is equivalent to the steady pressure term.
As is well known for steady flow that the zero free stream means zero lift. For unsteady flow however, during the vertical translation of the airfoil we expect to have a lift generation even under zero free stream. We can show this with a limiting process performed on the second term of Eq. 3.23 with multiplying the term with U2 and letting U go to zero as follows.
From the last line we see that the vertical force is proportional with s2za. Since za is independent of s then inverse Laplace transform of s2za gives us
![]() L {s2Za}
L {s2Za}
The last expression shows that even at zero free stream speed there exists a lifting force which is proportional to the acceleration in vertical translation. This force is an inertial force generated by the motion of the profile and it is called the apparent mass. Since there is no circulation attached to it, it is also called non circulatory term.
The third term at the right hand side of Eq. 3.23 is the circulatory term due to wake vortex sheet. For unsteady flows we do not have to take into consideration all three terms of Eq. 3.23. Depending on the unsteadiness we can ignore some of the terms in our analysis depending on the accuracy we look after. Now, we can discuss which term to neglect under what physical condition. According to a classical classification:
(i) ‘Unsteady aerodynamics’: All three terms are included. Motions with about 40 Hz frequencies are analyzed by this approach.
(ii) ‘Quasi unsteady aerodynamics’: The apparent mass term is neglected. Motions with 5-15 Hz frequencies are analyzed using this approach.
(iii) ‘Quasi steady aerodynamics’: Motions with frequency of 1 Hz or below is analyzed using the circulatory term only.
After making this classification, we can now derive a formula for the lifting pressure coefficient for simple harmonic motions and obtain the relevant aerodynamic coefficients such as sectional lift and moment coefficients.











