Unsteady Flow
IIn this section we are going to study, for the sake of completeness of the unsteady aerodynamic theory, the incompressible flow past some special planform undergoing time dependent motions. It has been shown that steady flow past a finite wing created zero spanwise vortex at the wake, yw = 0, and according to 4.7b chordwise vorticity at the wake was constant, i. e., = constant. For two
dimensional unsteady flow, the time variation of the effect of wake vorticity on the profile was reflected by Theodorsen function. Now, let us consider the effect of wake vorticity on the finite wing surface for simple harmonic motion. Let Ra
denote the wing surface and Rw the wake region for a wing whose surface motion is given by za(x, y, t) = Za(x, y)elxt. The downwash at the surface reads as
With the aid of 4.4, the amplitude of downwash in terms of vortex sheet strength becomes
– , Ї W f-a(i. g)(x – n)+-a(i. g)(y – Ц)лйл
![]() ”a(X, y)=-4-Jj [(Х-П)’^,^,^ d {dg
”a(X, y)=-4-Jj [(Х-П)’^,^,^ d {dg
Ra
– _L Z Ui. g)(x – fl + Mi;,g)(y- ()d {d,
4pR [(x – i)2 + (y – g)2]J/2
Ra
As we did before, to obtain the relation between the bound circulation Ca and the vortex sheet strength – w, we will, similarly, at a spanwise station g write the following relations in three dimensional case
xl(()
Here, the trailing edge is given by xt = xt(g).
— (( .xxL
Defining the reduced circulation as X(g) =-% ei и, the wake vortex sheet strength reads as – w(i, g) = —ik0X(g)e-i"U. The continuity of the vorticity, Odf = °(, once integrated with respect to n gives,
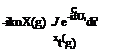 xt (g)
xt (g)
= 0( -(i’ g)di’+0(
xi (g)
![]()
![]()
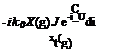 |
After performing last two integrals we obtain
Substituting these into 4.46 gives
![]() 1 Ui, g)(x – 0 + Шg)(y2- g)dndg
1 Ui, g)(x – 0 + Шg)(y2- g)dndg
![]() ApJ [(x – i)2 + (y – g)2]3/2
ApJ [(x – i)2 + (y – g)2]3/2
Ra
1 ff – x-ik°X(g)(x – n) +bodi(g1(y – g)A..A 4* JJ e " [(x – i)2 + (y – g)2]3/2 ig
Rw
The first integral of Eq. 4.47, using continuity of vorticity, can be written in terms of ya to obtain the integral equation between the downwash and the unknown bound vortex strength. As we did for the case of steady flow, we make some assumptions to simplify the double integrals. Let us now consider the Reissner’s simplifying approach as given in (BAH 1996).











